Voltage, Current, Resistance, and Ohm’s Law
Electricity Basics
When beginning to explore the world of electricity and electronics, it is vital to start by understanding the basics of voltage, current, and resistance.
These are the three basic building blocks required to manipulate and utilize electricity.
At first, these concepts can be challenging to understand because we cannot “see” them.
One cannot see the energy flowing through a wire or the voltage of a battery sitting on a table with the naked eye.
Even the lightning in the sky, while visible, is not truly the energy exchange happening from the clouds to the earth but a reaction in the air to the energy passing through it.
To detect this energy transfer, we must use measurement tools such as multimeters, spectrum analyzers, and oscilloscopes to visualize what is happening with the charge in a system.
Fear not; this tutorial will give you a basic understanding of voltage, current, and resistance and how the three relate to each other.
Electrical Charge
Electricity is the movement of electrons, and electrons create charge, which we can harness to do work.
Your lightbulb, stereo, phone, etc., harness the electrons’ movement to do work. They all operate using the same basic power source: the movement of electrons.
The three basic principles for this tutorial can be explained using electrons, or more specifically, the charge they create:
- Voltage is the difference in charge between two points.
- Current is the rate at which the charge is flowing.
- Resistance is a material’s tendency to resist the flow of charge (current).
So, when we talk about these values, we’re describing the movement of charge and, thus, the behavior of electrons.
A closed-loop circuit allows charges to move from one place to another. Components in the circuit allow us to control this charge and use it to do work.
Georg Ohm was a Bavarian scientist who studied electricity. Ohm begins by describing a unit of resistance that is defined by current and voltage. So, let’s start with voltage and go from there.
Voltage
We define voltage as the amount of potential energy between two points on a circuit. One point has more charge than another. This difference in charge between the two points is called voltage.
It is measured in volts, which, technically, is the potential energy difference between two points that will impart one joule of energy per coulomb of charge that passes through it (don’t panic if this makes no sense; we will explain all).
The unit “volt” is named after the Italian physicist Alessandro Volta, who invented what is considered the first chemical battery. Voltage is represented in equations and schematics by the letter “V.”
A common analogy is a water tank describing voltage, current, and resistance.
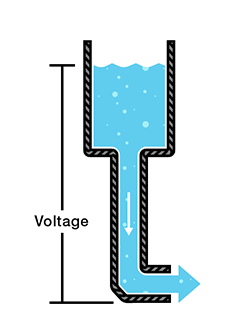In this analogy, the water amount represents charge, the water pressure represents voltage, and the water flow represents current.
So, for this analogy, remember:
Water = Charge
Pressure = Voltage
Flow = Current
Consider a water tank at a certain height above the ground.
At the bottom of this tank, there is a hose.
- The pressure at the end of the hose can represent voltage.
- The water in the tank represents charge.
- The more water in the tank, the higher the charge, the more pressure measured at the end of the hose.
We can think of this tank as a battery, a place where we store a certain amount of energy and then release it.
If we drain our tank a certain amount, the pressure created at the end of the hose goes down. We can think of this as decreasing voltage, like when a flashlight gets dimmer as the batteries run down.
There is also a decrease in the amount of water that will flow through the hose, and less pressure means less water is flowing, which brings us to the current.
Current
We can think of the amount of water flowing through the hose from the tank as current. The higher the pressure, the higher the flow, and vice-versa.
With water, we would measure the volume of the water flowing through the hose over a certain period of time.
With electricity, we measure the amount of charge flowing through the circuit over a period of time.
Current is measured in Amperes (usually just referred to as “Amps”).
An ampere is defined as 6.241*1018 electrons (1 Coulomb) per second passing through a point in a circuit. Amps are represented in equations by the letter “I.”
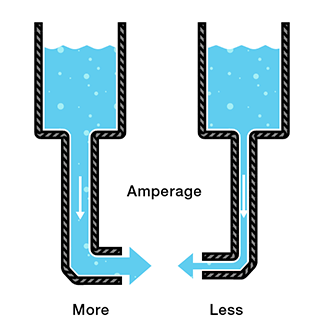
Let’s say we have two tanks, each with a hose from the bottom. Each tank has precisely the same amount of water, but the hose on one tank is narrower than the hose on the other.
We measure the same amount of pressure at the end of either hose, but when the water begins to flow, the flow rate of the water in the tank with the narrower hose will be less than the flow rate of the water in the tank with the wider hose.
In electrical terms, the current through the narrower hose is less than the current through the wider hose.
If we want the flow to be the same through both hoses, we have to increase the amount of water (charge) in the tank with the narrower hose.
This increases the pressure (voltage) at the end of the narrower hose, pushing more water through the tank.
This is analogous to an increase in voltage that causes an increase in current.
Now, we’re starting to see the relationship between voltage and current.
But there is a third factor to consider here: the width of the hose. In this analogy, the width of the hose is the resistance.
This means we need to add another term to our model:
- Water = Charge (measured in Coulombs)
- Pressure = Voltage (measured in Volts)
- Flow = Current (measured in Amperes, or “Amps” for short)
- Hose Width = Resistance
Resistance
Consider our two water tanks again, one with a narrow pipe and one with a wide pipe.
The tank with the narrow pipe creates a higher resistance.
It stands to reason that we can’t fit as much volume through a narrow pipe as through a wider one at the same pressure.
This is resistance.
The narrow pipe “resists” the flow of water through it even though the water is at the same pressure as the tank with the wider pipe.
In electrical terms, this is represented by two circuits with equal voltages and different resistances.
The circuit with the higher resistance will allow less charge to flow, meaning the circuit with higher resistance has less current flowing through it.
This brings us to Georg Ohm. Ohm defines the unit of resistance of “1 Ohm” as the resistance between two points in a conductor where the application of 1 volt will push 1 ampere or 6.241×1018 electrons.
This value is usually represented in schematics with the Greek letter “Ω,” which is called omega and pronounced “ohm.”
Ohm’s Law
Georg Ohm (March 16, 1789, to July 6, 1854, Munich), a German physicist who discovered the law named after him, stated that the current flow through a conductor is directly proportional to the potential difference (voltage) and inversely proportional to the resistance.
Combining the elements of voltage, current, and resistance, Ohm developed the formula:
V = I x R
Where
- V = Voltage in volts
- I = Current in amps
- R = resistance in ohms
This is called Ohm’s law.
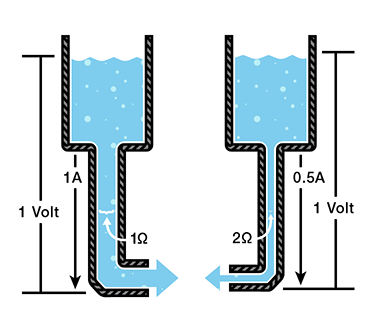
Let’s say, for example, that we have a circuit with the potential of 1 volt, a current of 1 amp, and a resistance of 1 ohm.
Using Ohm’s Law, we can say: 1V = 1A x 1Ω
Let’s say this represents our tank with a wide hose.
The amount of water in the tank is defined as 1 volt, and the “narrowness” (resistance to flow) of the hose is defined as 1 ohm.
Using Ohms Law gives us a flow (current) of 1 amp.
Let’s now look at the tank with the narrow hose using this analogy. Because the hose is narrower, its resistance to flow is higher.
Let’s define this resistance as 2 ohms.
The amount of water in the tank is the same as the other tank, so using Ohm’s Law, our equation for the tank with the narrow hose is
But what is the current? 1V = ?A x 2Ω
Because the resistance is greater and the voltage is the same, this gives us a current value of 0.5 amps: 1V = 0.5A x 2Ω
So, the current is lower in the tank with higher resistance.
Now, we can see that if we know two of the values for Ohm’s law, we can solve for the third.
Why is Ohm’s law so fundamental?
Ohm’s law states the relationship between voltage (V), current (I), and resistance (R).
The equation is simplified as V = I x R, which can be used in AC and DC circuits.
This law explains how the most important concepts of electricity relate to each other. It is beneficial because it helps us calculate currents and voltages in circuits.
Without Ohm’s law, there will be no electricity at all.
Therefore, the major importance of this law is that it allows us to enjoy the uses of our appliances now, such as TVs, refrigerators, players, etc.
Ohm’s law is also applied in circuit connections, such as computing the power equation.
With this, it is easier to understand how to wire electrical components without the fear of low voltage or electric shock.
If Ohm’s law is understood, parallel or series wiring can be applied appropriately.
By applying Ohm’s law, one can determine how much voltage is used in the circuits, how much current can be applied, or what kind of resistance will be used.
There are three variables in the equation, so if one variable is missing, it is easier to compute by using the equation.
Ohm’s law not only determines the voltage of a particular appliance but can also verify the current or resistance.
If the voltage and resistance are given, the current can be measured; if the current and voltage are present, the resistance can still be measured.
This is how Ohm’s law works and why you cannot underestimate its importance.
A Real-world example of why you should know ohms law is:
Suppose you had to install a ten-horsepower 1ø motor for an exhaust fan, and it was 100′ away from a power source.
Would you
- A) Operate the motor at 115 volts (100 amps), or
- B) Operate the motor at 230 volts (50 amps).
The wattage would be the same for both applications.
You’ll need to run #3 copper in the first example and, in the second, #8 copper.
One costs twice as much (or close to it) as the other one does. Ultimately, this is an example of Ohm’s law and why it’ll be essential to know it later.
Ohms Law Relationship
By knowing any two values of the Voltage, Current, or Resistance quantities, we can use Ohms Law to find the third missing value.
Ohms Law is used extensively in electronic formulas and calculations, so it is “crucial to understand and accurately remember these formulas.”
To find the Voltage ( V )
[ V = I x R ] V (volts) = I (amps) x R (Ω)
To find the Current ( I )
[ I = V ÷ R ] I (amps) = V (volts) ÷ R (Ω)
To find the Resistance ( R )
[ R = V ÷ I ] R (Ω) = V (volts) ÷ I (amps)
It is sometimes easier to remember Ohms’s law relationship by using pictures.
Here, the three quantities of V, I, and R have been superimposed into a triangle (affectionately called the Ohms Law Triangle), giving voltage at the top with current and resistance at the bottom.
This arrangement represents the actual position of each quantity in the Ohms law formulas.
Transposing the above Ohms Law equation gives us the following combinations of the same equation:
Then, by using Ohms Law, we can see that a voltage of 1V applied to a resistor of 1Ω will cause a current of 1A to flow, and the greater the resistance, the less current will flow for any applied voltage.
Any Electrical device or component that obeys “Ohm’s Law” that is, the current flowing through it is proportional to the voltage across it ( I α V ), such as resistors or cables, are said to be “Ohmic” in nature, and devices that do not, such as transistors or diodes, are said to be “Non-ohmic” devices.
Electrical Power in Circuits
Electrical Power ( P ) in a circuit is the amount of energy absorbed or produced within the circuit.
A source of energy such as a voltage will produce or deliver power while the connected load absorbs it.
Light bulbs and heaters, for example, absorb power and convert it into heat or light, and the higher their value or rating in watts, the more power they will consume.
The quantity symbol for power is P and is the product of voltage multiplied by the current, with the unit of measurement being the
- Watt ( W ) with prefixes used to denote
- milliwatts (mW = 10-3W) or
- kilowatts (kW = 103W).
Then, by using Ohm’s law and substituting for V, I, and R, the formula for electrical power can be found as follows:
To find the Power (P)
[ P = V x I ] P (watts) = V (volts) x I (amps)
Also,
[ P = V2 ÷ R ] P (watts) = V2 (volts) ÷ R (Ω)
Also,
[ P = I2 x R ] P (watts) = I2 (amps) x R (Ω)
Again, the three quantities have been superimposed into the Power Triangle, with power at the top and current and voltage at the bottom.
Again, this arrangement represents the actual position of each quantity in the Ohms law power formulas.
The Power Triangle
transposing the basic Ohms Law equation above for power gives us the following combinations of the same equation to find the various individual quantities:
So, we can see that there are three possible formulas for calculating electrical power in a circuit.
The component absorbs the power if the calculated power is positive (+P) in value for any formula. That is, it is consuming or using power.
But if the calculated power is negative (-P) in value, the component produces or generates power. In other words, it is a source of electrical power, such as batteries and generators.
Power Rating
Electrical components are given a “power rating” in watts that indicates the maximum rate at which the component converts the electrical power into other forms of energy, such as heat, light, or motion.
Examples are a 1/4W resistor, a 100W light bulb, etc.
Electrical devices convert one form of power into another; for example, an electrical motor will convert electrical energy into a mechanical force, an electrical generator converts mechanical force into electrical energy, and a light bulb converts electrical energy into both light and heat.
Also, we now know that the power unit is the watt, but some electrical devices, such as electric motors, have a power rating in the old “Horsepower” or hp measurement.
The relationship between horsepower and watts is given as 1hp = 746W.
So, for example, a two-horsepower motor has a rating of 1492W (2 x 746) or 1.5kW.
Ohms Law Pie Chart
To help us understand the relationship between the various values a little further, we can take all of Ohm’s Law equations from above for finding Voltage, Current, Resistance, and Power and condense them into a simple Ohms Law pie chart for use in AC and DC circuits and calculations as shown.
Ohms Law Matrix Table
As well as using the Ohm’s Law Pie Chart shown above, you can also put the individual Ohm’s Law equations into a simple matrix table as shown for easy reference when calculating an unknown value.
Ohms Law Example
For the circuit shown below, find:
The Voltage (V), the current (I), the Resistance (R), and the Power (P).
- Voltage [ V = I x R ] = 2 x 12Ω = 24V
- Current [ I = V ÷ R ] = 24 ÷ 12Ω = 2A
- Resistance [ R = V ÷ I ] = 24 ÷ 2 = 12 Ω
- Power [ P = V x I ] = 24 x 2 = 48W
Power within an electrical circuit is only present when BOTH voltage and current are present. For example,
In an Open-circuit condition, Voltage is present, but there is no current flow I = 0 (zero); therefore, V x 0 is 0, so the power dissipated within the circuit must also be 0.
Likewise, if we have a Short-circuit condition, current flow is present, but there is no voltage V = 0. Therefore, 0 x I = 0, the power dissipated within the circuit is 0.
As electrical power is the product of V x I, the power dissipated in a circuit is the same whether the circuit contains high voltage and low current or low voltage and high current flow.
Generally, power is dissipated in the form of
- Heat (heaters),
- Mechanical Work such as motors, etc.,
- Energy in the form of radiated (Lamps) or
- as stored energy (Batteries).
Electrical Energy in Circuits
Electrical Energy is the capacity to do work, and the unit of work or energy is the joule ( J ).
Electrical energy is the product of power multiplied by the length of time it is consumed.
So if we know how much power in Watts is being consumed and the time, in seconds, for which it is used, we can find the total energy used in watt-seconds.
In other words, Energy = power x time and Power = voltage x current.
Therefore, electrical power is related to energy, and the unit given for electrical energy is the watt-seconds or joules.
Electrical energy = Power (W) x Time(s)
Electrical power can also be defined as the transfer rate of energy.
If one joule of work is absorbed or delivered at a constant rate of one second, the corresponding power will be equivalent to one watt. Power can be defined as “1Joule/sec = 1Watt”.
Then, we can say that one watt is equal to one joule per second, and electrical power can be defined as the rate of doing work or the transfer of energy.
Electrical Power and Energy Triangle
Or to find the various individual quantities:
We said previously that electrical energy is defined as watts per second or joules.
Although electrical energy is measured in Joules, it can become a considerable value when used to calculate the energy consumed by a component.
For example, if a 100-watt light bulb is left-” ON” for 24 hours, the energy consumed will be 8,640,000 Joules (100W x 86,400 seconds), so prefixes such as kilojoules (kJ = 103J) or megajoules (MJ = 106J) are used instead, and in this simple example, the energy consumed will be 8.64MJ (megajoules).
When dealing with joules, kilojoules, or megajoules to express electrical energy, the math involved can end up with huge numbers and lots of zeros.
It is easier to express electrical energy consumed in Kilowatt-hours when the electrical power consumed (or generated) is measured in watts or kilowatts (thousands of watts) and measured in hours, not seconds. The unit of electrical energy will be the kilowatt-hours (kWhr).
Then our 100-watt light bulb above will consume 2,400 watt-hours or 2.4kWhr, which is much easier to understand than the 8,640,000 joules.
One kWhr is the amount of electricity used by a device rated at 1000 watts in one hour. It is commonly called a “Unit of Electricity,” This is measured by the utility meter and is what consumers purchase from their electricity suppliers.
Kilowatt-hours are the standard units of energy used by the electricity meter in our homes to calculate the amount of electrical energy we use and, therefore, how much we pay.
So if you switched on an electric heater with an element rated at 1000 watts and left it on for 1 hour, you will have consumed one kWh of electricity.
If you switched on two electric fires, each with 1000-watt elements, for half an hour, the total consumption would be precisely the same amount of electricity – 1kWh.
So, consuming 1000 watts for one hour uses the same amount of power as 2000 watts (twice as much) for half an hour (half the time).
Then, for a 100-watt light bulb to use one kWhr or one unit of electrical energy, it would need to be switched on for a total of 10 hours (10 x 100 = 1000 = 1kWh).
Ohm’s Law and its correct use are central to an electrical training course.
While learning Ohm’s Law and putting it into practice, there’s one rule to know:
Always sketch a rough diagram of the circuit you are considering before you start making calculations based on the values in the circuit that are already known to you.
This rule becomes essential when circuits become more complex.
- Use Your Head
- Time and effort can be saved by intelligent use of Ohm’s Law.
If you are trying to find the voltage existing across a parallel circuit, You can obtain a direct voltmeter reading without any need for disconnection.
However, the use of Ohm’s Law will often give you the information you want without the need for an actual measurement.