ALTERNATING CURRENT
INTRODUCTION
The material covered in this lesson contains many new terms that are explained as you progress through the material.
We review the differences between ac and dc voltage and current as well as the advantages of ac power transmission over dc power transmission. we also review the “left-hand rule” for a conductor and the relationship between current and magnetism.
We also cover the methods by which ac power can be generated and the relationship between frequency, period, time, and wavelength.
Finally, we compute peak-to-peak, instantaneous, effective, and average values of voltage and current and the phase difference between sine waves.
ALTERNATING CURRENT
A companion lesson to Basic DC Current. AC AND DC Alternating current is current which constantly changes in amplitude and which reverses direction at regular intervals. Direct current flows only in one direction and the amplitude of the current is determined by the number of electrons flowing past a point in a circuit in one second. If, for example, a coulomb of electrons moves past a point in a wire in one second and all of the electrons are moving in the same direction, the amplitude of direct current in the wire is one ampere.
Similarly, if half a coulomb of electrons moves in one direction past a point in the wire in half a second, then reverses direction and moves past the same point in the opposite direction during the next half-second, a total of one coulomb of electrons passes the point in one second. The amplitude of the alternating current is one ampere. The preceding comparison of dc and ac is illustrated. Notice that one white arrow plus one striped arrow comprise one coulomb.
DISADVANTAGES OF DC COMPARED TO AC
When commercial use of electricity became widespread in the United States, certain disadvantages in using direct current in the home became apparent.
If a commercial direct-current system is used, the voltage must be generated at the level (amplitude or value) required by the load. To properly light a 240- volt lamp, for example, the dc generator must deliver 240 volts. If a 120-volt lamp is to be supplied power from the 240-volt generator, a resistor or another 120-volt lamp must be placed in series with the 120-volt lamp to drop the extra 120 volts.
When the resistor is used to reduce the voltage, an amount of power equal to that consumed by the lamp is wasted.
Another disadvantage of the direct-current system becomes evident when the direct current (I) from the generating station must be transmitted a long distance over wires to the consumer. When this happens, a large amount of power is lost due to the resistance (R) of the wire. The power loss is equal to I2R. However, this loss can be greatly reduced if the power is transmitted over the lines at a very high voltage level and a low current level. This is not a practical solution to the power loss in the dc system since the load would then have to be operated at a dangerously high voltage.
Because of the disadvantages related to transmitting and using direct current, practically all modern commercial electric power companies generate and distribute alternating current (ac). Unlike direct voltages, alternating voltages can be stepped up or down in amplitude by a device called a TRANSFORMER. (The transformer will be explained later in this lesson.)
The use of the transformer permits efficient transmission of electrical power over long-distance lines. At the electrical power station, the transformer output power is at high voltage and low current levels. At the consumer end of the transmission lines, the voltage is stepped down by a transformer to the value required by the load. Due to its inherent advantages and versatility, alternating current has replaced direct current in all but a few commercial power distribution systems.
VOLTAGE WAVEFORMS
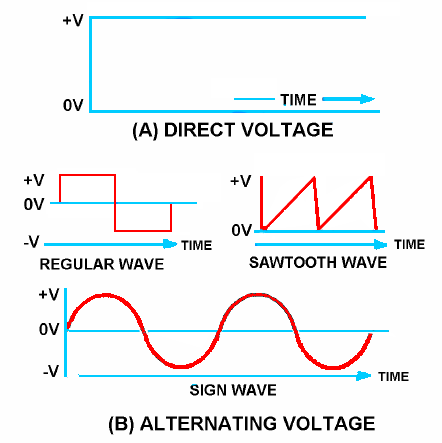
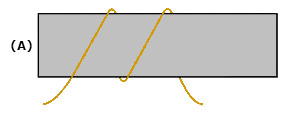
You now know that there are two types of current and voltage, that is, direct current and voltage and alternating current and voltage. If a graph is constructed showing the amplitude of a dc voltage across the terminals of a battery with respect to time, it will appear in figure 1 view A.
The dc voltage is shown to have a constant amplitude. Some voltages go through periodic changes in amplitude like those shown in figure 1 view B. The pattern which results when these changes in amplitude with respect to time are plotted on graph paper is known as a WAVEFORM.
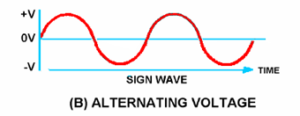
Figure 1 view B shows some of the common electrical waveforms. Of those illustrated, the sine wave will be dealt with most often.
ELECTROMAGNETISM
The sine wave illustrated in figure 1 view B is a plot of a current that changes amplitude and direction.
Although there are several ways of producing this current, the method based on the principles of electromagnetic induction is by far the easiest and most common method in use.
The fundamental theories concerning simple magnets and magnetism were discussed in Basic Electrical Theory, but how magnetism can be used to produce electricity was only briefly mentioned.
This lesson will give you a more in-depth study of magnetism. The main points that will be explained are how magnetism is affected by an electric current and, conversely, how electricity is affected by magnetism.
This general subject area is most often referred to as ELECTROMAGNETISM. To properly understand electricity, you must first become familiar with the relationships between magnetism and electricity.
For example, you must know that:
- An electric current always produces some form of magnetism.
- The most commonly used means for producing or using electricity involves magnetism.
- The peculiar behavior of electricity under certain conditions is caused by magnetic influences.
When a compass is placed in the vicinity of a current-carrying conductor, the needle aligns itself at right angles to the conductor. The north pole of the compass indicates the direction of the magnetic field produced by the current.
By knowing the direction of current, you can use the left-hand rule for conductors to determine the direction of the magnetic lines of force.
Arrows are generally used in electrical diagrams to indicate the direction of current in a wire. A cross (+) on the end of a cross-sectional view of a wire indicates that current is flowing away from you, while a dot (·) indicates that current is flowing toward you.
When two adjacent parallel conductors carry current in the same direction, the magnetic fields around the conductors aid each other. When the currents in the two conductors flow in opposite directions, the fields around the conductors oppose each other.
MAGNETIC FIELDS
In 1819 Hans Christian Oersted, a Danish physicist found that a definite relationship exists between magnetism and electricity. He discovered that an electric current is always accompanied by certain magnetic effects and that these effects obey definite laws.
MAGNETIC FIELD AROUND A CURRENT-CARRYING CONDUCTOR
If a compass is placed in the vicinity of a current-carrying conductor, the compass needle will align itself at right angles to the conductor, thus indicating the presence of a magnetic force. You can demonstrate the presence of this force by using the arrangement illustrated in figure 2.
In figure 2 (A), the needle deflections show that a magnetic field exists in circular form around the conductor.
When the current flows upward (see figure 2(A), the direction of the field is clockwise, as viewed from the top.
However, if you reverse the polarity of the battery so that the current flows downward (see figure 2(B), the direction of the field is counterclockwise.
The relation between the direction of the magnetic lines of force around a conductor and the direction of electron current flow in the conductor may be determined by means of the LEFT-HAND RULE FOR A CONDUCTOR:
If you grasp the conductor in your left hand with the thumb extended in the direction of the electron flow (current) (− to +), your fingers will point in the direction of the magnetic lines of force. Now apply this rule to figure 2.
Note that your fingers point in the direction that the north pole of the compass points when it is placed in the magnetic field surrounding the wire.
An arrow is generally used in electrical diagrams to denote the direction of current in a length of wire (see figure 3(A).
Where a cross-section of a wire is shown, an end view of the arrow is used. A cross-sectional view of a conductor that is carrying current toward the observer is illustrated in figure 3(B).
Notice that the direction of the current is indicated by a dot, representing the head of the arrow. A conductor that is carrying current away from the observer is illustrated in figure 3(C).
Note that the direction of the current is indicated by a cross, representing the tail of the arrow. Also, note that the magnetic field around a current-carrying conductor is perpendicular to the conductor and that the magnetic lines of force are equal along all parts of the conductor. When two adjacent parallel conductors are carrying current in the same direction, the magnetic lines of force combine and increase the strength of the field around the conductors, as shown in figure 4(A).
Two parallel conductors carrying currents in opposite directions are shown in figure 4(B).
Note that the field around one conductor is opposite in direction to the field around the other conductor. The resulting lines of force oppose each other in the space between the wires, thus deforming the field around each conductor. This means that if two parallel and adjacent conductors are carrying currents in the same direction, the fields about the two conductors aid each other.
Conversely, if the two conductors are carrying currents in opposite directions, the fields about the conductors repel each other.
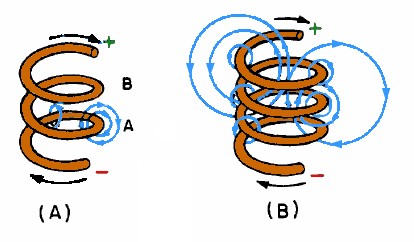
MAGNETIC FIELD OF A COIL
When a wire is wound around a core, it forms a COIL.
The magnetic fields are produced when current flows in the coil combine. The combined influence of all of the fields around the turns produces a two-pole field similar to that of a simple bar magnet. When the direction of current in the coil is reversed, the polarity of the two-pole field of the coil is reversed.
The strength of the magnetic field of the coil is dependent upon:
- The number of turns of the wire in the coil.
- The amount of current in the coil.
- The ratio of the coil length to the coil width.
- The type of material in the core.
When current is passed through the coil, the magnetic field about each turn of wire links with the fields of the adjacent turns The combined influence of all the turns produces a two-pole field similar to that of a simple bar magnet.
- Figure 3(A) illustrates that the magnetic field around a current-carrying wire exists at all points along the wire.
- Figure 5 illustrates that when a straight wire is wound around a core, it forms a coil and that the magnetic field about the core assumes a different shape.
- Figure 5(A) is actually a partial cutaway view showing the construction of a simple coil.
- Figure 5(B) shows a cross-sectional view of the same coil.
- Notice that the two ends of the coil are identified as X and Y.
One end of the coil is a north pole, and the other end is a south pole. The polarity of an Electromagnetic Coil Figure 2 shows that the direction of the magnetic field around a straight wire depends on the direction of current in that wire.
Thus, a reversal of current in a wire causes a reversal in the direction of the magnetic field that is produced. It follows that a reversal of the current in a coil also causes a reversal of the two-pole magnetic field about the coil.
When the direction of the current in a coil is known, you can determine the magnetic polarity of the coil by using the LEFT-HAND RULE FOR COILS.
This rule, illustrated in figure 6, is stated as follows:
Grasp the coil in your left hand with your fingers “wrapped around” in the direction of the electron current flow. Your thumb will then point toward the north pole of the coil.
Strength of an Electromagnetic Field
The strength or intensity of a coil’s magnetic field depends on a number of factors. The main ones are listed below and will be discussed again later.
- The number of turns of wire in the coil.
- The amount of current flowing in the coil.
- The ratio of the coil length to the coil width.
- The type of material in the core.
Losses in an Electromagnetic Field
When current flows in a conductor, the atoms in the conductor all line up in a definite direction, producing a magnetic field.
When the direction of the current changes, the direction of the atoms’ alignment also changes, causing the magnetic field to change direction.
To reverse all the atoms requires that power be expended, and this power is lost.
This loss of power (in the form of heat) is called HYSTERESIS LOSS.
Hysteresis loss is common to all ac equipment; however, it causes few problems except in motors, generators, and transformers.
When these devices are discussed later in this lesson, hysteresis loss will be covered in more detail.
BASIC AC GENERATION
From the previous discussion, you learned that a current-carrying conductor produces a magnetic field around itself.
Under-producing a voltage (emf) using magnetism, you learned how a changing magnetic field produces an emf in a conductor. That is if a conductor is placed in a magnetic field, and either the field or the conductor moves, an emf is induced in the conductor.
This effect is called electromagnetic induction.
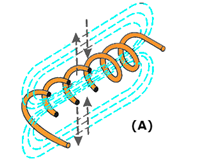
CYCLE
Figures 7 and 8 show a suspended loop of wire (conductor) being rotated (moved) in a clockwise direction through the magnetic field between the poles of a permanent magnet.
For ease of explanation, the loop has been divided into a dark half and light half.
Notice in (A) of the figure that the dark half is moving along (parallel to) the lines of force.
Consequently, it is cutting NO lines of force. The same is true of the light half, which is moving in the opposite direction. Since the conductors are cutting, no lines of force, no emf is induced.
As the loop rotates toward the position shown in (B), it cuts more and more lines of force per second (inducing an ever-increasing voltage) because it is cutting more directly across the field (lines of force).
At (B), the conductor is shown completing one-quarter of a complete revolution, or 90º, of a complete circle.
Because the conductor is now cutting directly across the field, the voltage induced in the conductor is maximum.
When the value of induced voltage at various points during the rotation from (A) to (B) is plotted on a graph (and the points connected), a curve appears as shown below.
As the loop continues to be rotated toward the position shown below in (C), it cuts fewer and fewer lines of force. The induced voltage decreases from its peak value.
Eventually, the loop is once again moving in a plane parallel to the magnetic field, and no emf is induced in the conductor.
The loop has now been rotated through half a circle (one alternation or 180º). If the preceding quarter-cycle is plotted, it appears as shown below.
When the same procedure is applied to the second half of rotation (180º through 360º), the curve appears as shown below.
Notice the only difference is in the polarity of the induced voltage. Where previously the polarity was positive, it is now negative. The sine curve shows the value of induced voltage at each instant of time during the rotation of the loop.
Notice that this curve contains 360º or two alternations.
TWO ALTERNATIONS represent ONE complete CYCLE of rotation.
Assuming a closed path is provided across the ends of the conductor loop, you can determine the direction of current in the loop by using the LEFT-HAND RULE FOR GENERATORS.
The two induced voltages in the loop add together to form one total emf. It is this emf that causes the current in the loop.
When the loop rotates to the position shown in (D) of figure 8, the action reverses. The dark half is moving up instead of down, and the light half is moving down instead of up.
By applying the left-hand rule once again, you will see that the total induced emf and its resulting current have reversed direction. The voltage builds up to maximum in this new direction, as shown by the sine curve in figure 8.
The loop finally returns to its original position (E), at which point voltage is again zero. The sine curve represents one complete cycle of voltage generated by the rotating loop.
All the illustrations used in this chapter show the wire loop moving in a clockwise direction. In actual practice, the loop can be moved clockwise or counterclockwise.
Regardless of the direction of movement, the left-hand rule applies.
If the loop is rotated through 360º at a steady rate, and if the strength of the magnetic field is uniform, the voltage produced is a sine wave of voltage. Continuous rotation of the loop will produce a series of sine-wave voltage cycles or, in other words, an ac voltage.
As mentioned previously, the cycle consists of two complete alternations in a period of time.
Recently the HERTZ (Hz) has been designated to indicate one cycle per second. If ONE CYCLE PER SECOND is ONE HERTZ, then 100 cycles per second are equal to 100 hertz, and so on.
Throughout these modules, the term cycle is used when no specific time element is involved, and the term Hertz (Hz) is used when the time element is measured in seconds.
FREQUENCY
If the loop in figure 8 (A) makes one complete revolution each second, the generator produces one complete cycle of ac during each second (1 Hz).
Increasing the number of revolutions to two per second will produce two complete cycles of ac per second (2 Hz).
The number of complete cycles of alternating current or voltage completed each second is referred to as the FREQUENCY.
Frequency is always measured and expressed in hertz.
Alternating-current frequency is an important term to understand since most ac electrical equipment requires a specific frequency for proper operation.
PERIOD
The time required to complete one cycle of a waveform is called the PERIOD OF THE WAVE.
Each ac sine wave is composed of two alternations.
- The alternation which occurs during the time the sine wave is positive is called the positive alternation.
- The alternation which occurs during the time the sine wave is negative is called the negative alternation.
- In each cycle of sine wave, the two alternations are identical in size and shape, but opposite in polarity.
- The period of a sine wave is inversely proportional to the frequency; e.g., the higher the frequency, the shorter the period.
An individual cycle of any sine wave represents a definite amount of TIME.
Notice that figure 9 shows 2 cycles of a sine wave which has a frequency of 2 hertz (Hz).
Figure 9.—Period of a sine wave.
Since 2 cycles occur each second, 1 one cycle of a waveform is called the PERIOD of the wave.
In figure 10, the period is one-half second.
The relationship between time (t) and frequency (f) is indicated by the formula.
Where t = period in seconds and
f = Frequency in hertz
Each cycle of the sine wave shown in figure 10 consists of two identically shaped variations in voltage.
- The variation which occurs during the time the voltage is positive is called the POSITIVE ALTERNATION.
- The variation which occurs during the time the voltage is negative is called the NEGATIVE ALTERNATION.
- In a sine wave, these two alternations are identical in size and shape, but opposite in polarity.
- The distance from zero to the maximum value of each alternation is called the AMPLITUDE.
- The amplitude of the positive alternation and the amplitude of the negative alternation is the same.
WAVELENGTH
The time it takes for a sine wave to complete one cycle is defined as the period of the waveform.
The distance traveled by the sine wave during this period is referred to as WAVELENGTH. Wavelength indicated by the symbol λ (Greek lambda), is the distance along the waveform from one point to the same point on the next cycle.
You can observe this relationship by examining figure 10.
The point on the waveform that measurement of wavelength begins is not important as long as the distance is measured to the same point on the next cycle (see figure 11).
ALTERNATING CURRENT VALUES
In discussing alternating current and voltage, you will often find it necessary to express the current and voltage in terms of MAXIMUM or PEAK values, PEAK-to-PEAK values, EFFECTIVE values, AVERAGE values, or INSTANTANEOUS values.
Each of these values has a different meaning and is used to describe a different amount of current or voltage.
PEAK AND PEAK-TO-PEAK VALUES Refer to figure 12. Notice it shows the positive alternation of a sine wave (a half-cycle of ac) and a dc waveform that occur simultaneously.
Note that the dc starts and stops at the same moment, as does the positive alternation and that both waveforms rise to the same maximum value.
However, the dc values are greater than the corresponding ac values at all points except the point at which the positive alternation passes through its maximum value.
At this point, the dc and ac values are equal. This point on the sine wave is referred to as the maximum or peak value.
During each complete cycle of ac, there are always two maximum or peak values, one for the positive half-cycle and the other for the negative half-cycle.
The difference between the peak positive value and the peak negative value is called the peak-to-peak value of the sine wave.
This value is twice the maximum or peak value of the sine wave and is sometimes used for the measurement of ac voltages. Note the difference between peak and peak-to-peak values in figure 13.
Usually, alternating voltage and current are expressed in EFFECTIVE VALUES (a term you will study later) rather than in peak-to-peak values.
INSTANTANEOUS VALUE
The INSTANTANEOUS value of an alternating voltage or current is the value of voltage or current at one particular instant. The value may be zero if the particular instant is the time in the cycle at which the polarity of the voltage is changing.
It may also be the same as the peak value if the selected instant is the time in the cycle at which the voltage or current stops increasing and starts decreasing.
There are actually an infinite number of instantaneous values between zero and the peak value.
AVERAGE VALUE
The AVERAGE value of an alternating current or voltage is the average of ALL the INSTANTANEOUS values during ONE alternation.
Since the voltage increases from zero to peak value and decreases back to zero during one alternation, the average value must be some value between those two limits.
You could determine the average value by adding together a series of instantaneous values of the alternation (between 0º and 180º) and then dividing the sum by the number of instantaneous values used.
The computation would show that one alternation of a sine wave has an average value equal to 0.636 times the peak value.
The formula for average voltage is
Eavg = 0.636 × Emax
where Eavg is the average voltage of one alternation, and Emax is the maximum or peak voltage.
Similarly, the formula for average current is
Iavg = 0.636 × Imax
where Iavg is the average current in one alternation, and Imax is the maximum or peak current.
Do not confuse the above definition of an average value with that of the average value of a complete cycle.
Because the voltage is positive during one alternation and negative during the other alternation, the average value of the voltage values occurring during the complete cycle is zero.
EFFECTIVE VALUE OF A SINE WAVE
Emax, Eavg, Imax, and Iavg are values used in ac measurements.
Another value used is the EFFECTIVE value of ac.
This is the value of alternating voltage or current that will have the same effect on resistance as a comparable value of direct voltage or current will have on the same resistance.
In an earlier discussion you were told that when current flows in a resistance, heat is produced. When direct current flows in a resistance, the amount of electrical power converted into heat equals I2R watts.
However, since an alternating current having a maximum value of 1 ampere does not maintain a constant value, the alternating current will not produce as much heat in the resistance as produced by a direct current of 1 ampere.
Figure 14 compares the heating effect of 1 ampere of dc to the heating effect of 1 ampere of ac.
Examine views A and B of figure 1-15 and notice that the heat (70.7º C) produced by 1 ampere of alternating current (that is, an ac with a maximum value of 1 ampere) is only 70.7 percent of the heat (100º C) produced by 1 ampere of direct current.
Mathematically,
Therefore, for effective value of ac (Ieff) = 0.707 × Imax.
The rate at which heat is produced in a resistance forms a convenient basis for establishing an effective value of alternating current and is known as the “heating effect” method.
An alternating current is said to have an effective value of one ampere when it produces heat in a given resistance at the same rate as does one ampere of direct current.
You can compute the effective value of a sine wave of current to a fair degree of accuracy by taking equally-spaced instantaneous values of current along the curve and extracting the square root of the average of the sum of the squared values.
For this reason, the effective value is often called the “root-mean-square” (rms) value.
Thus,
Stated another way, the effective or rms value (Ieff) of a sine wave of current is 0.707 times the maximum value of current (Imax).
Thus, Ieff = 0.707 × Imax. When I eff is known, you can find Imax by using the formula Imax = 1.414 × Ieff.
You might wonder where the constant 1.414 comes from. To find out, examine figure 1-14 again and read the following explanation.
Assume that the dc in figure 1-14(A) is maintained at 1 ampere and the resistor temperature at 100º C. Also, assume that the ac in figure 1-14(B) is increased until the temperature of the resistor is 100º C.
At this point, it is found that a maximum ac value of 1.414 amperes is required in order to have the same heating effect as direct current. Therefore, in the ac circuit, the maximum current required is 1.414 times the effective current.
It is important for you to remember the above relationship and that the effective value (Ieff) of any sine wave of current is always 0.707 times the maximum value (Imax).
Since alternating current is caused by an alternating voltage, the ratio of the effective value of voltage to the maximum value of voltage is the same as the ratio of the effective value of current to the maximum value of current.
Stated another way, the effective or rms value (Eeff) of a sine-wave of voltage is 0.707 times the maximum value of voltage (Emax),
Thus,
When an alternating current or voltage value is specified in a book or on a diagram, the value is an effective value unless there is a definite statement to the contrary.
Remember that all meters, unless marked to the contrary, are calibrated to indicate effective values of current and voltage.
Problem: A circuit is known to have an alternating voltage of 120 volts and a peak or maximum current of 30 amperes.
What are the peak voltage and effective current values?
SINE WAVES IN PHASE
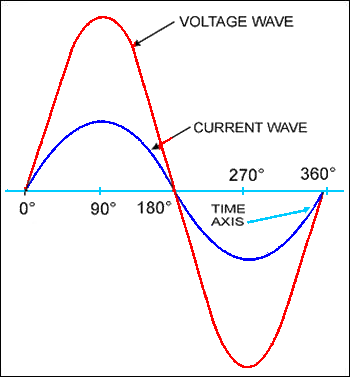
When a sine wave of voltage is applied to resistance, the resulting current is also a sine wave. This follows Ohm’s law which states that current is directly proportional to the applied voltage.
Now examine figure 15.
Notice that the sine wave of voltage and the resulting sine wave of current is superimposed on the same time axis.
Notice also that as the voltage increases in a positive direction, the current increases along with it, and that when the voltage reverses direction, the current also reverses direction.
When two sine waves are precisely in step with one another, they are said to be IN PHASE. To be in phase, the two sine waves must go through their maximum and minimum points at the same time and in the same direction
SINE WAVES OUT OF PHASE
When two sine waves go through their minimum and maximum points at different times, a phase difference exists between them.
Figure 16 shows voltage wave E 1 which is considered to start at 0º (time one).
As voltage wave E1 reaches its positive peak, voltage wave E2 starts its rise (time two).
Since these voltage waves do not go through their maximum and minimum points at the same instant of time, a PHASE DIFFERENCE exists between the two waves.
The two waves are said to be OUT OF PHASE. For the two waves in figure 17, the phase difference is 90º.
To further describe the phase relationship between two sine waves, the terms LEAD and LAG are used. The amount by which one sine wave leads or lags another sine wave is measured in degrees.
Refer again to figure 18. Observe that wave E2 starts 90º later in time than does wave E1.
You can also describe this relationship by saying that wave E1 leads wave E2 by 90º, or that wave E2 lags wave E1 by 90º (Either statement is correct; it is the phase relationship between the two sine waves that is important.)
It is possible for one sine wave to lead or lag another sine wave by any number of degrees, except 0º or 360º. When the latter condition exists, the two waves are said to be in phase.
Thus, two sine waves that differ in phase by 45º are actually out of phase with each other, whereas two sine waves that differ in phase by 360º are considered to be in phase with each other.
A phase relationship that is quite common is shown in figure 18. Notice that the two waves illustrated differ in phase by 180º.
Notice also that although the waves pass through their maximum and minimum values at the same time, their instantaneous voltages are always of opposite polarity.
If two such waves exist across the same component, and the waves are of equal amplitude, they cancel each other.
When they have different amplitudes, the resultant wave has the same polarity as the larger wave and has an amplitude equal to the difference between the amplitudes of the two waves.
To determine the phase difference between two sine waves, locate the points on the time axis where the two waves cross the time axis traveling in the same direction.
The number of degrees between the crossing points is the phase difference.
The wave that crosses the axis at the later time (to the right on the time axis) is said to lag the other wave.
OHM’S LAW IN AC CIRCUITS
Many ac circuits contain resistance only.
The rules for these circuits are the same rules that apply to dc circuits.
Resistors, lamps, and heating elements are examples of resistive elements.
When an ac circuit contains only resistance, Ohm’s Law, Kirchhoff’s Law, and the various rules that apply to voltage, current, and power in a dc circuit also apply to the ac circuit.
The Ohm’s Law formula for an ac circuit can be stated as
Remember, unless otherwise stated, all ac voltage and current values are given as effective values.
The formula for Ohm’s Law can also be stated as
The important thing to keep in mind is: Do Not mix ac values.
When you solve for effective values, all values you use in the formula must be effective values.
Similarly, when you solve for average values, all values you use must be average values. This point should be clearer after you work on the following problem:
A series circuit consists of two resistors (R1 = 5 ohms and R2 = 15 ohms) and an alternating voltage source of 120 volts. What is Iavg?
The alternating voltage is assumed to be an effective value (since it is not specified to be otherwise).
Apply the Ohm’s Law formula.
The problem, however, asked for the average value of current (I avg).
To convert the effective value of current to the average value of current, you must first determine the peak or maximum value of current, Imax.
You can now find Iavg.
Just substitute 8.484 amperes in the Iavg formula and solve for Iavg.
Remember, you can use the Ohm’s Law formulas to solve any purely resistive ac circuit problem. Use the formulas in the same manner as you would solve a dc circuit problem.
VOLTAGE WAVEFORMS – The waveform of voltage or current is a graphical picture of changes in voltage or current values over a period of time. Figure 19.
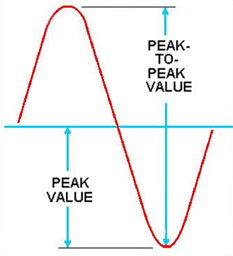
PEAK AND PEAK-TO-PEAK VALUES
The maximum value reached during one alternation of a sine wave is the peak value. The maximum reached during the positive alternation to the maximum value reached during the negative alternation is the peak-to-peak value.
The peak-to-peak value is twice the peak value. Figure 20.
EFFECTIVE VALUE OF AN ALTERNATING CURRENT
The effective value of an alternating current or voltage is the value of alternating current or voltage that produces the same amount of heat in a resistive component that would be produced in the same component by a direct current or voltage of the same value.
The effective value of a sine wave is equal to 0.707 times the peak value. The effective value is also called the root mean square or rms value.
The term rms value is used to describe the process of determining the effective value of a sine wave by using the instantaneous value of voltage or current.
You can find the rms value of a current or voltage by taking equally spaced instantaneous values on the sine wave and extracting the square root of the
average of the sum of the instantaneous values.
This is where the term “Root-Mean-Square” (rms) value comes from.
The formulas for effective and maximum values of voltage and current are:
Alternating Current and Transformers
Inductance
Inductance is the property of a coil that causes energy to be stored in a magnetic field about the coil. The energy is stored so as to oppose any change in current.
The study of inductance is a challenging but rewarding segment of electricity. It is challenging because at first, it seems that new concepts are being introduced. However, these new concepts are merely extensions of fundamental principles already covered in this TC.
The study of inductance is rewarding because a thorough understanding of it will enable you to acquire a working knowledge of electrical circuits more rapidly.
This lesson defines inductance and describes the factors that affect it.
CHARACTERISTICS OF INDUCTANCE
Inductance is the characteristic of an electrical circuit that opposes the starting, stopping, or changing of current flow.
- The symbol for inductance is L.
- The basic unit of inductance is the henry (H).
One henry equals the inductance required to induce 1 volt in an inductor by a change of current of 1 ampere per second.
An analogy of inductance is found in pushing a heavy load (such as a wheelbarrow or car). It takes more work to start the load than it does to keep it moving.
Once the load starts to move, it is easier to keep the load moving than to stop it again. This is because the load possesses the property of inertia.
- Inertia is the characteristic of mass that opposes a change in velocity.
Inductance has the same effect on current in an electrical circuit as inertia has when moving a mechanical object. It requires more energy to start or stop current than it does to keep it flowing.
ELECTROMOTIVE FORCE
Electromotive force is developed whenever there is relative motion between a magnetic field and a conductor.
Electromotive force is a difference of potential or voltage which exists between two points in an electrical circuit.
In generators and inductors, the emf is developed by the action between the magnetic field and the electrons in a conductor.
Figure 21 shows that an inductor is a wire that is coiled (such as in a relay coil, motor, or transformer) shows EMF generated in an electrical conductor.
When a magnetic field moves through a stationary metallic conductor, electrons are dislodged from their orbits. The electrons move in a direction determined by the movement of the magnetic lines of flux.
This is shown below:
The electrons move from one area of the conductor into another area.
- The area that the electrons moved from has fewer negative charges (electrons) and becomes positively charged.
- The area the electrons move into becomes negatively charged.
This is shown below:
The difference between the charges in the conductor is equal to a difference of potential (or voltage).
This voltage caused by the moving magnetic field is called electromotive force (emf).
In simple terms, the action of a moving magnetic field on a conductor can be compared to the action of a broom.
Consider the moving magnetic field to be a moving broom.
As the magnetic broom moves along (through) the conductor, it gathers up and pushes electrons before it, as shown below:
The area from which electrons are moved becomes positively charged, while the area into which electrons are moved becomes negatively charged.
The potential difference between these two areas is the electromotive force or emf.
SELF-INDUCTANCE
Even a perfectly straight length of conductor has some inductance.
As you know, current in a conductor produces a magnetic field surrounding the conductor.
When the current changes, the magnetic field changes.
This causes relative motion between the magnetic field and the conductor, and an electromotive force (emf) is induced in the conductor.
This emf is called a SELF-INDUCED EMF because it is induced in the conductor carrying the current.
The emf produced by this moving magnetic field is also referred to as COUNTER ELECTROMOTIVE FORCE (cemf).
To understand what CEMF is and how it develops, first review a basic requirement for the production of voltage.
To produce a voltage or EMF magnetically, there must be the following:
- A conductor.
- A magnetic field.
- Relative motion.
Next, review some of the properties of an electrical circuit.
DO NOT connect the ends of a length of wire to a terminal of an AC generator. This will cause an electrical short where maximum current would flow.
The excessive current would flow because there would be only the minimal resistance of the wire to hold back the current. This will damage the electrical system.
The polarity of the counter electromotive force is in the opposite direction to the applied voltage of the conductor.
The overall effect will be to oppose a change in current magnitude.
This effect is summarized by Lenz’s law which states:
THE INDUCED EMF IN ANY CIRCUIT IS ALWAYS IN A DIRECTION TO OPPOSE THE EFFECT THAT PRODUCED IT.
If the shape of the conductor is changed to form a loop, then the electromagnetic field around each portion of the conductor cuts across some other portion of the same conductor.
This is shown in its simplest form in figure 22 A & B.
A length of conductor is looped so that two portions of the conductor lie next to each other. These portions are labeled conductor 1 and conductor 2.
When the switch is closed, current (electron flow) in the conductor produces a magnetic field around ALL portions of the conductor. For simplicity, the magnetic field (expanding lines of flux) is shown in a single plane that is perpendicular to both conductors.
Although the expanding field of flux originates at the same time in both conductors, it is considered as originating in conductor 1 and its effect on conductor 2 will be explained.
With increasing current, the flux field expands outward from conductor 1, cutting across a portion of conductor 2. This results in an induced emf in conductor 2 as shown by the dashed arrow.
Note that the induced emf is in the opposite direction to (in OPPOSITION to) the battery current and voltage, as stated in Lenz’s law.
The direction of this induced voltage may be determined by applying the LEFT-HAND RULE FOR GENERATORS. This rule is applied to a portion of conductor 2 that is “lifted” and enlarged for this purpose in figure 22(A).
This rule states that if you point the thumb of your left hand in the direction of relative motion of the conductor and your index finger in the direction of the magnetic field, your middle finger, extended as shown, will now indicate the direction of the induced current which will generate the induced voltage (cemf) as shown.
In figure 22(B), the same section of conductor 2 is shown after the switch has been opened. The flux field is collapsing.
Applying the left-hand rule, in this case, shows that the reversal of flux MOVEMENT has caused a reversal in the direction of the induced voltage. The induced voltage is now in the same direction as the battery voltage.
The most important thing for you to note is that the self-induced voltage opposes BOTH changes in current. That is, when the switch is closed, this voltage delays the initial buildup of current by opposing the battery voltage.
When the switch is opened, it keeps the current flowing in the same direction by aiding the battery voltage. Thus, from the above explanation, you can see that when a current is building up it produces an expanding magnetic field.
This field induces an emf in the direction opposite to the actual flow of current.
This induced emf opposes the growth of the current and the growth of the magnetic field. If the increasing current had not set up a magnetic field, there would have been no opposition to its growth.
The whole reaction, or opposition, is caused by the creation or collapse of the magnetic field, the lines of which as they expand or contract cut across the conductor and develop the counter emf.
Since all circuits have conductors in them, you can assume that all circuits have inductance. However, inductance has its greatest effect only when there is a change in current.
Inductance does NOT oppose current, only a CHANGE in current. Where current is constantly changing as in an ac circuit, inductance has more effect.
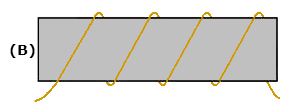
To increase the property of inductance, the conductor can be formed into a loop or coil. A coil is also called an inductor.
Figure 23 shows a conductor formed into a coil.
Current through one loop produces a magnetic field that encircles the loop in the direction as shown in figure 23(A).
- As current increases, the magnetic field expands and cuts all the loops as shown in figure 23(B).
- The current in each loop affects all other loops.
- The field cutting the other loop has the effect of increasing the opposition to a current change.
Inductors are classified according to core type.
- The core is the center of the inductor just as the core of an apple is the center of an apple.
- The inductor is made by forming a coil of wire around a core.
- The core material is normally one of two basic types: soft-iron or air.
An iron-core inductor and its schematic symbol (which is represented with lines across the top of it to indicate the presence of an iron core) are shown, in figure 24(A).
The air-core inductor may be nothing more than a coil of wire, but it is usually a coil formed around a hollow form of some nonmagnetic material such as cardboard.
This material serves no purpose other than to hold the shape of the coil. An air-core inductor and its schematic symbol are shown in figure 4(B)
Figure 24B.—Inductor types and schematic symbols.
Factors Affecting Coil Inductance
There are several physical factors that affect the inductance of a coil.
They include the number of turns in the coil, the diameter of the coil, the coil length, the type of material used in the core, and the number of layers of winding in the coils.
Inductance depends entirely upon the physical construction of the circuit, and can only be measured with special laboratory instruments.
Of the factors mentioned, consider first how the number of turns affects the inductance of a coil.
Figure 25(A)(B) shows two coils.
- Coil (A) has two turns. In coil (A), the flux field set up by one loop cuts one other loop.
- Coil (B) has four turns. In coil (B), the flux field set up by one loop cuts three other loops
Doubling the number of turns in the coil will produce a field twice as strong if the same current is used.
A field twice as strong, cutting twice the number of turns, will induce four times the voltage. Therefore, it can be said that the inductance varies as the square of the number of turns.
The second factor is the coil diameter.
In figure 26 you can see that the coil in view B has twice the diameter of coil view A.
Figure 26.—Inductance factor (diameter).
Physically, it requires more wire to construct a coil of large diameter than one of small diameter with an equal number of turns. Therefore, more lines of force exist to induce a counter emf in the coil with the larger diameter.
Actually, the inductance of a coil increases directly as the cross-sectional area of the core increases. Recall the formula for the area of a circle: A = πr2.
Doubling the radius of a coil increases the inductance by a factor of four.
The third factor that affects the inductance of a coil is the length of the coil. Figure 27 (A) (B) shows two examples of coil spacing.
Coil (A) has three turns, rather widely spaced, making a relatively long coil. A coil of this type has few flux linkages, due to the greater distance between each turn.
Therefore, coil (A) has a relatively low inductance. Coil (B) has closely spaced turns, making a relatively short coil.
This close spacing increases the flux linkage, increasing the inductance of the coil. Doubling the length of a coil while keeping the same number of turns halves the value of inductance.
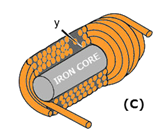
The fourth physical factor is the type of core material used with the coil. Figure 28 shows two coils:
Coil (A) with an air core, and coil (B) with a soft-iron core. The magnetic core of coil (B) is a better path for magnetic lines of force than is the nonmagnetic core of coil (A).
The soft-iron magnetic core’s high permeability has less reluctance to the magnetic flux, resulting in more magnetic lines of force.
This increase in the magnetic lines of force increases the number of lines of force cutting each loop of the coil, thus increasing the inductance of the coil.
It should now be apparent that the inductance of a coil increases directly as the permeability of the core material increases.
Another way of increasing the inductance is to wind the coil in layers. Figure 29 shows three cores with different amounts of layering.
The coil in figure 29(A) is a poor inductor compared to the others in the figure because its turns are widely spaced and there is no layering.
The flux movement, indicated by the dashed arrows, does not link effectively because there is only one layer of turns.
A more inductive coil is shown in figure 29(B).
The turns are closely spaced and the wire has been wound in two layers. The two layers link each other with a greater number of flux loops during all flux movements.
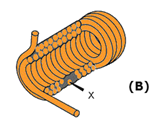
Note that nearly all the turns, such as X, are next to four other turns (shaded). This causes the flux linkage to be increased. A coil can be made still more inductive by winding it in three layers, as shown in figure 29(C).
The increased number of layers (cross-sectional area) improves flux linkage even more.
Note that some turns, such as Y, lie directly next to six other turns (shaded). In actual practice, layering can continue on through many more layers. The important fact to remember, however, is that the inductance of the coil increases with each layer added.
As you have seen, several factors can affect the inductance of a coil, and all of these factors are variable. Many differently constructed coils can have the same inductance.
The important information to remember, however, is that inductance is dependent upon the degree of linkage between the wire conductor(s) and the electromagnetic field. In a straight length of conductor, there is very little flux linkage between one part of the conductor and another.
Therefore, its inductance is extremely small. It was shown that conductors become much more inductive when they are wound into coils. This is true because there is maximum flux linkage between the conductor turns, which lie side by side in the coil.
UNIT OF INDUCTANCE
As stated before, the basic unit of inductance (L) is the HENRY (H), named after Joseph Henry, the co-discoverer with Faraday of the principle of electromagnetic induction.
An inductor has an inductance of 1 henry if an emf of 1 volt is induced in the inductor when the current through the inductor is changing at the rate of 1 ampere per second.
The relationship between the induced voltage, the inductance, and the rate of change of current with respect to time is stated mathematically as:
where ( Eind ) is the induced emf in volts; ( L ) is the inductance in henrys, and ( ΔI ) is the change in current in amperes occurring in ( Δt )seconds.
The symbol (Δ) (Greek letter delta), means “a change in ….”.
The henry is a large unit of inductance and is used with relatively large inductors. With small inductors, millihenry is used.
(A millihenry is equal to 1 × 10-3 henry, and one henry is equal to 1,000 millihenrys.)
For still smaller inductors the unit of inductance is the microhenry (μH).
(A μH = 1 × 10 -6H, and one henry is equal to 1,000,000 microhenrys.)
GROWTH AND DECAY OF CURRENT IN AN LR SERIES CIRCUIT
When a battery is connected across a “pure” inductance, the current builds up to its final value at a rate determined by the battery voltage and the internal resistance of the battery.
The current buildup is gradual because of the counter emf generated by the self-inductance of the coil. When the current starts to flow, the magnetic lines of force move outward from the coil.
These lines cut the turns of wire on the inductor and build up a counter emf that opposes the emf of the battery.
This opposition causes a delay in the time it takes the current to build up to a steady value When the battery is disconnected, the lines of force collapse.
Again these lines cut the turns of the inductor and build up an emf that tends to prolong the flow of current.
A voltage divider containing resistance and inductance may be connected in a circuit by means of a special switch, as shown in figure 30(A).
Such a series arrangement is called an LR series circuit.
When switch S1 is closed (as shown), a voltage ES appears across the voltage divider.
At this instant, the current will attempt to increase to its maximum value.
However, this instantaneous current change causes coil L to produce a back EMF, which is opposite in polarity and almost equal to the EMF of the source.
This back EMF opposes the rapid current change.
Figure 30(B) shows that at the instant switch S1 is closed, there is no measurable growth current (ig), a minimum voltage drop is across resistor R, and maximum voltage exists across inductor L.
Electrical inductance is like mechanical inertia, and the growth of current in an inductive circuit can be likened to the acceleration of a boat on the surface of the water.
The boat does not move at the instant a constant force is applied to it. At this instant, all the applied force is used to overcome the inertia of the boat. Once the inertia is overcome the boat will start to move.
After a while, the speed of the boat reaches its maximum value and the applied force is used up in overcoming the friction of the water against the hull.
When the battery switch (S1) in the LR circuit of figure 30(A) is closed, the rate of the current increase is maximum in the inductive circuit.
At this instant, all the battery voltage is used in overcoming the emf of self-induction which is a maximum because the rate of change of current is maximum.
Thus the battery voltage is equal to the drop across the inductor and the voltage across the resistor is zero.
As time goes on more of the battery voltage appears across the resistor and less across the inductor.
The rate of change of current is less and the induced emf is less. As the steady-state condition of the current is approached, the drop across the inductor approaches zero and all of the battery voltage is “dropped” across the resistance of the circuit.
Thus the voltages across the inductor and the resistor change in magnitude during the period of growth of current the same way the force applied to the boat divides itself between the effects of inertia and friction.
In both examples, the force is developed first across the inertia/inductive effect and finally across the friction/resistive effect.
Figure 30(C) shows that when switch S2 is closed (source voltage ES removed from the circuit), the flux that has been established around the inductor (L) collapses through the windings.
This induces a voltage eL in the inductor that has a polarity opposite to ES and is essentially equal to ES in magnitude.
The induced voltage causes decay current (id) to flow in resistor R in the same direction in which current was flowing originally (when S1 was closed).
A voltage (eR) that is initially equal to source voltage (ES) is developed across R.
The voltage across the resistor (eR) rapidly falls to zero as the voltage across the inductor (eL) falls to zero due to the collapsing flux.
Just as the example of the boat was used to explain the growth of current in a circuit, it can also be used to explain the decay of current in a circuit.
When the force applied to the boat is removed, the boat still continues to move through the water for a while, eventually coming to a stop.
This is because energy was being stored in the inertia of the moving boat. After a period of time, the friction of the water overcomes the inertia of the boat, and the boat stops moving.
Just as inertia of the boat stored energy, the magnetic field of an inductor stores energy.
Because of this, even when the power source is removed, the stored energy of the magnetic field of the inductor tends to keep current flowing in the circuit until the magnetic field collapse.
L/R Time Constant
The L/R TIME CONSTANT is a valuable tool for use in determining the time required for current in an inductor to reach a specific value.
As shown in figure 31, one L/R time constant is the time required for the current in an inductor to increase to 63 percent (actually 63.2 percent) of the maximum current.
The following example should clear up any confusion about time constants. Assume that maximum current in an LR circuit is 10 amperes. As you know, when the circuit is energized, it takes time for the current to go from zero to 10 amperes.
When the first time constant is completed, the current in the circuit is equal to 63.2% of 10 amperes. Thus the amplitude of current at the end of 1 time constant is 6.32 amperes.
During the second time constant, current again increases by 63.2% (.632) of the difference in value between the current flowing in the inductor and the maximum current.
This difference is 10 amperes minus 6.32 amperes and equals 3.68 amperes; 63.2% of 3.68 amperes is 2.32 amperes. This increase in current during the second time constant is added to that of the first time constant. Thus, upon completion of the second time constant, the amount of current in the LR circuit is 6.32 amperes + 2.32 amperes = 8.64 amperes.
During the third constant, current again increases:
- 10 amperes -8.64 amperes = 1.36 amperes
- 1.36 amperes x .632 = 0.860
- 864 amperes + 0.860 amperes = 9.50 amperes
During the fourth time constant, current again increases:
- 10 amperes -9.50 amperes = 0.5 amperes
- 0.5 amperes x .632 = 0.316
- 9.50 amperes + 0.316 amperes = 9.82 amperes
During the fifth time constant, current increases as before:
- 10 amperes -9.82 amperes = 0.18 amperes
- 0.18 amperes x .632 = 0.114
- 9.82 amperes + 0.114 amperes = 9.93 amperes
Thus, the current at the end of the fifth time constant is almost equal to 10.0 amperes, the maximum current. For all practical purposes, the slight difference in value can be ignored. When an LR circuit is de-energized, the circuit current decreases (decays) to zero in five-time constants at the same rate that it previously increased. If the growth and decay of current in an LR circuit are plotted on a graph, the curve appears as shown in figure 11.
Notice that current increases and decays at the same rate in five-time constants. The value of the time constant in seconds is equal to the inductance in henrys divided by the circuit resistance in ohms.
The formula used to calculate one L/R time constant is:
POWER LOSS IN AN INDUCTOR
Since an inductor (coil) consists of a number of turns of wire, and since all wire has some resistance, every inductor has a certain amount of resistance. Normally this resistance is small.
It is usually neglected in solving various types of ac circuit problems because the reactance of the inductor (the opposition to alternating current, which will be discussed later) is so much greater than the resistance that the resistance has a negligible effect on the current.
However, since some inductors are designed to carry relatively large amounts of current, considerable power can be dissipated in the inductor even though the amount of resistance in the inductor is small.
This power is wasted power and is called COPPER LOSS. The copper loss of an inductor can be calculated by multiplying the square of the current in the inductor by the resistance of the winding (I2R). In addition to copper loss, an iron-core coil (inductor) has two iron losses.
These are called HYSTERESIS LOSS and EDDY-CURRENT LOSS.
Hysteresis loss is due to power that is consumed in reversing the magnetic field of the inductor core each time the direction of current in the inductor changes. Eddy-current loss is due to heating of the core by circulating currents that are induced in the iron core by the magnetic field around the turns of the coil.
These currents are called eddy currents and circulate within the iron core only. All these losses dissipate power in the form of heat. Since this power cannot be returned to the electrical circuit, it is lost power.
MUTUAL INDUCTANCE
Whenever two coils are located so that the flux from one coil links with the turns of the other coil, a change of flux in one coil causes an emf to be induced in the other coil. This allows the energy from one coil to be transferred or coupled to the other coil.
The two coils are said to be coupled or linked by the property of MUTUAL INDUCTANCE (M). The amount of mutual inductance depends on the relative positions of the two coils. This is shown in figure 12.
If the coils are separated a considerable distance, the amount of flux common to both coils is small and the mutual inductance is low. Conversely, if the coils are close together so that nearly all the flux of one coil links the turns of the other, the mutual inductance is high.
The mutual inductance can be increased greatly by mounting the coils on a common iron core. Two coils are placed close together as shown in figure 33 (A) (B).
If switch S is now opened as in figure 33(B), the ammeter (A) deflects momentarily in the opposite direction, indicating a momentary flow of current in the opposite direction in coil 2. This current in coil 2 is produced by the collapsing magnetic field of coil 1.
FACTORS AFFECTING MUTUAL INDUCTANCE
The mutual inductance of two adjacent coils is dependent upon the physical dimensions of the two coils, the number of turns in each coil, the distance between the two coils, the relative positions of the axes of the two coils, and the permeability of the cores.
The COEFFICIENT OF COUPLING between two coils is equal to the ratio of the flux cutting one coil to the flux originated in the other coil.
If the two coils are so positioned with respect to each other so that all of the flux of one coil cuts all of the turns of the other, the coils are said to have a unity coefficient of coupling.
It is never exactly equal to unity (1), but it approaches this value in certain types of coupling devices.
If all of the flux produced by one coil cuts only half the turns of the other coil, the coefficient of coupling is 0.5.
The coefficient of coupling is designated by the letter K.
The mutual inductance between two coils, L1 and L2, is expressed in terms of the inductance of each coil and the coefficient of coupling K.
As a formula:
Example problem: One 10-H coil and one 20-H coil are connected in series and are physically close enough to each other so that their coefficient of coupling is 0.5.
What is the mutual inductance between the coils?
SERIES INDUCTORS WITHOUT MAGNETIC COUPLING
When inductors are well shielded or are located far enough apart from one another, the effect of mutual inductance is negligible.
If there is no mutual inductance (magnetic coupling) and the inductors are connected in series, the total inductance is equal to the sum of the individual inductances.
As a formula:
LT = L1 + L2 + L3 +…LN
where LT is the total inductance; L1, L2, L3 are the inductances of L1, L2, L3; and Ln means that any number (n) of inductors may be used.
The inductances of inductors in series are added together like the resistances of resistors in series.
SERIES INDUCTORS WITH MAGNETIC COUPLING
When two inductors in series are so arranged that the field of one links the other, the combined inductance is determined as follows:
The plus sign is used with M when the magnetic fields of the two inductors are aiding each other, as shown in figure 34.
Capacitance
Capacitance is the ability of a body to store an electrical charge. Any object that can be electrically charged exhibits capacitance.
In the previous lesson, you learned that inductance is the property of a coil that causes electrical energy to be stored in a magnetic field about the coil. The energy is stored in such a way as to oppose any change in current.
CAPACITANCE is similar to inductance because it also causes storage of energy. A CAPACITOR is a device that stores electrical energy in an ELECTROSTATIC FIELD. The energy is stored in such a way as to oppose any change in voltage.
Just how capacitance opposes a change in voltage is explained later in this chapter. However, it is first necessary to explain the principles of an electrostatic field as it is applied to capacitance.
THE ELECTROSTATIC FIELD
You previously learned that opposite electrical charges attract each other while like electrical charges repel each other.
The reason for this is the existence of an electrostatic field.
Any charged particle is surrounded by invisible lines of force, called electrostatic lines of force.
These lines of force have some interesting characteristics:
- They are polarized from positive to negative.
- They radiate from a charged particle in straight lines and do not form closed loops.
- They have the ability to pass through any known material.
- They have the ability to distort the orbits of tightly bound electrons.
Examine figure 35.
This figure represents two unlike charges surrounded by their electrostatic field.
Because an electrostatic field is polarized positive to negative, arrows are shown radiating away from the positive charge and toward the negative charge.
Stated another way, the field from the positive charge is pushing, while the field from the negative charge is pulling.
The effect of the field is to push and pull the unlike charges together. In figure 36, two like charges are shown with their surrounding electrostatic field.
If two, unlike charges, are placed on opposite sides of an atom whose outermost electrons cannot escape their orbits, the orbits of the electrons are distorted as shown in figure 36.
Figure 37(A) shows the normal orbit. Part (B) of the figure shows the same orbit in the presence of charged particles. Since the electron is a negative charge, the positive charge attracts the electrons, pulling the electrons closer to the positive charge.
The negative charge repels the electrons, pushing them further from the negative charge. It is this ability of an electrostatic field to attract and to repel charges that allow the capacitor to store energy.
THE SIMPLE CAPACITOR
A simple capacitor consists of two metal plates separated by an insulating material called a dielectric, as illustrated in figure 38.
Note that one plate is connected to the positive terminal of a battery; the other plate is connected through a closed switch (S1) to the negative terminal of the battery.
Remember, an insulator is a material whose electrons cannot easily escape their orbits.
Due to the battery voltage, plate A is charged positively and plate B is charged negatively. (How this happens is explained later in this lesson.)
Thus an electrostatic field is set up between the positive and negative plates.
The electrons on the negative plate (plate B) are attracted to the positive charges on the positive plate (plate A).
Notice that the orbits of the electrons in the dielectric material are distorted by the electrostatic field.
The distortion occurs because the electrons in the dielectric are attracted to the top plate while being repelled from the bottom plate.
When switch S1 is opened, the battery is removed from the circuit and the charge is retained by the capacitor.
This occurs because the dielectric material is an insulator, and the electrons in the bottom plate (negative charge) have no path to reach the top plate (positive charge).
The distorted orbits of the atoms of the dielectric plus the electrostatic force of attraction between the two plates hold the positive and negative charges in their original position.
Thus, the energy which came from the battery is now stored in the electrostatic field of the capacitor.
Two slightly different symbols for representing a capacitor are shown in figure 39.
Notice that each symbol is composed of two plates separated by a space that represents the dielectric.
The curved plate in (B) of the figure indicates the plate should be connected to a negative polarity.
THE FARAD
Capacitance is measured in units called FARADS.
One-farad capacitor stores one coulomb (a unit of charge (Q) equal to 6.28 × 1018 electrons) of charge when a potential of 1 volt is applied across the terminals of the capacitor.
This can be expressed by the formula:
The farad is a very large unit of measurement of capacitance.
For convenience, the microfarad (abbreviated µF) or the picofarad (abbreviated µP) or 1 × 10–6 farad, and 1.0 picofarad is equal to 0.000000000001 farad or 1.0 × 10–12 farad.
Capacitance is a physical property of the capacitor and does not depend on circuit characteristics of voltage, current, and resistance.
A given capacitor always has the same value of capacitance (farads) in one circuit as in any other circuit in which it is connected.
FACTORS AFFECTING THE VALUE OF CAPACITANCE
The value of capacitance of a capacitor depends on three factors:
- The area of the plates.
- The distance between the plates.
- The dielectric constant of the material between the plates.
PLATE AREA affects the value of capacitance in the same manner that the size of a container affects the amount of water that can be held by the container.
A capacitor with a large plate area can store more charges than a capacitor with a small plate area.
Simply stated, “the larger the plate area, the larger the capacitance”.
The second factor affecting capacitance is the DISTANCE BETWEEN THE PLATES. Electrostatic lines of force are strongest when the charged particles that create them are close together. When the charged particles are moved further apart, the lines of force weaken, and the ability to store a charge decreases.
The third factor affecting capacitance is the DIELECTRIC CONSTANT of the insulating material between the plates of a capacitor. The various insulating materials used as the dielectric in a capacitor differ in their ability to respond to (pass) electrostatic lines of force.
A dielectric material, or insulator, is rated as to its ability to respond to electrostatic lines of force in terms of a figure called the DIELECTRIC CONSTANT.
A dielectric material with a high dielectric constant is a better insulator than a dielectric material with a low dielectric constant.
Dielectric constants for some common materials are given in the following list:
Notice the dielectric constant for a vacuum. Since a vacuum is the standard of reference, it is assigned a constant of one.
The dielectric constants of all materials are compared to that of a vacuum.
Since the dielectric constant of air has been determined to be approximately the same as that of a vacuum, the dielectric constant of AIR is also considered to be equal to one.
The formula used to compute the value of capacitance is:
0, 2249 = a constant resulting from conversion from Metric to English units.
Example: Find the capacitance of a parallel plate capacitor with paraffin paper as the dielectric.
Given: K = 3.5
d = 0.05
A = 12 square inches
By examining the above formula you can see that capacitance varies directly as the dielectric constant and the area of the capacitor plates, and inversely as the distance between the plates.
VOLTAGE RATING OF CAPACITORS
In selecting or substituting a capacitor for use, consideration must be given to
- The value of capacitance desired and
- The amount of voltage to be applied across the capacitor.
If the voltage applied across the capacitor is too great, the dielectric will break down, and arcing will occur between the capacitor plates.
When this happens the capacitor becomes a short-circuit and the flow of direct current through it can cause damage to other electronic parts. Each capacitor has a voltage rating (a working voltage) that should not be exceeded.
The working voltage of the capacitor is the maximum voltage that can be steadily applied without danger of breaking down the dielectric. The working voltage depends on the type of material used as the dielectric and on the thickness of the dialectic.
(A high-voltage capacitor that has a thick dielectric must have a relatively large plate area in order to have the same capacitance as a similar low-voltage capacitor having a thin dielectric.)
The working voltage also depends on the applied frequency because the losses, and the resultant heating effect, increase as the frequency increases.
A capacitor with a voltage rating of 500 volts dc cannot be safely subjected to an alternating voltage or a pulsating direct voltage having an effective value of 500 volts.
Since an alternating voltage of 500 volts (rms) has a peak value of 707 volts, a capacitor to which it is applied should have a working voltage of at least 750 volts.
In practice, a capacitor should be selected so that its working voltage is at least 50 percent greater than the highest effective voltage to be applied to it.
CAPACITOR LOSSES
Power loss in a capacitor may be attributed to dielectric hysteresis and dielectric leakage. Dielectric hysteresis may be defined as an effect in a dielectric material similar to the hysteresis found in a magnetic material.
It is the result of changes in orientation of electron orbits in the dielectric because of the rapid reversals of the polarity of the line voltage.
The amount of power loss due to dielectric hysteresis depends upon the type of dielectric used. A vacuum dielectric has the smallest power loss.
Dielectric leakage occurs in a capacitor as the result of LEAKAGE CURRENT through the dielectric. Normally it is assumed that the dielectric will effectively prevent the flow of current through the capacitor.
Although the resistance of the dielectric is extremely high, a minute amount of current does flow. Ordinarily, this current is so small that for all practical purposes it is ignored.
However, if the leakage through the dielectric is abnormally high, there will be a rapid loss of charge and an overheating of the capacitor.
The power loss of a capacitor is determined by loss in the dielectric. If the loss is negligible and the capacitor returns the total charge to the circuit, it is considered to be a perfect capacitor with a power loss of zero.
CHARGING AND DISCHARGING A CAPACITOR
CHARGING: In order to better understand the action of a capacitor in conjunction with other components, the charge and discharge actions of a purely capacitive circuit are analyzed first.
For ease of explanation, the capacitor and voltage source shown in figure 40 are assumed to be perfect (no internal resistance), although this is impossible in practice.
In figure 40(A), an uncharged capacitor is shown connected to a four-position switch. With the switch in position 1, the circuit is open and no voltage is applied to the capacitor.
With the switch in position 1, the circuit is open and no voltage is applied to the capacitor.
Initially, each plate of the capacitor is a neutral body and until a difference of potential is impressed across the capacitor, no electrostatic field can exist between the plates.
To CHARGE the capacitor, the switch must be thrown to position 2, which places the capacitor across the terminals of the battery.
Under the assumed perfect conditions, the capacitor would reach full charge instantaneously.
However, the charging action is spread out over a period of time in the following discussion so that a step-by-step analysis can be made.
At the instant the switch is thrown to position 2, figure-40 (B), a displacement of electrons occurs simultaneously in all parts of the circuit.
This electron displacement is directed away from the negative terminal and toward the positive terminal of the source (the battery). A brief surge of current will flow as the capacitor charges.
If it were possible to analyze the motion of the individual electrons in this surge of charging current, the following action would be observed. See figure 41. At the instant the switch is closed, the positive terminal of the battery extracts an electron from the bottom conductor.
The negative terminal of the battery forces an electron into the top conductor. At this same instant, an electron is forced into the top plate of the capacitor and another is pulled from the bottom plate.
Thus, in every part of the circuit, a clockwise DISPLACEMENT of electrons occurs simultaneously.
As electrons accumulate on the top plate of the capacitor and others depart from the bottom plate, a difference of potential develops across the capacitor.
Each electron forced onto the top plate makes that plate more negative, while each electron removed from the bottom causes the bottom plate to become more positive.
Notice that the polarity of the voltage which builds up across the capacitor is such as to oppose the source voltage. The source voltage (emf) forces current around the circuit of figure 41 in a clockwise direction.
The emf developed across the capacitor, however, has a tendency to force the current in a counterclockwise direction, opposing the source emf.
As the capacitor continues to charge, the voltage across the capacitor rises until it is equal to the source voltage.
Once the capacitor voltage equals the source voltage, the two voltages balance one another and current ceases to flow in the circuit.
In studying the charging process of a capacitor, you must be aware that NO current flows THROUGH the capacitor. The material between the plates of the capacitor must be an insulator.
However, to an observer stationed at the source or along one of the circuit conductors, the action has all the appearances of a true flow of current, even though the insulating material between the plates of the capacitor prevents the current from having a complete path.
The current which appears to flow through a capacitor is called DISPLACEMENT CURRENT.
When a capacitor is fully charged and the source voltage is equaled by the counter electromotive force (cemf) across the capacitor, the electrostatic field between the plates of the capacitor is maximum. Figure 42.
Since the electrostatic field is maximum the energy stored in the dielectric is also maximum. If the switch is now opened as shown in figure 43(A), the electrons on the upper plate are isolated.
The electrons on the top plate are attracted to the charged bottom plate.
Because the dielectric is an insulator, the electrons cannot cross the dielectric to the bottom plate. The charges on both plates will be effectively trapped by the electrostatic field and the capacitor will remain charged indefinitely.
You should note at this point that the insulating dielectric material in a practical capacitor is not perfect and small leakage current will flow through the dielectric.
This current will eventually dissipate the charge. However, a high-quality capacitor may hold its charge for a month or more.
- To review briefly, when a capacitor is connected across a voltage source, a surge of charging current flows.
- This charging current develops a cemf across the capacitor which opposes the applied voltage.
- When the capacitor is fully charged, the cemf is equal to the applied voltage, and charging current ceases.
- At full charge, the electrostatic field between the plates is at maximum intensity and the energy stored in the dielectric is maximum.
- If the charged capacitor is disconnected from the source, the charge will be retained for some period of time.
- The length of time the charge is retained depends on the amount of leakage current present.
- Since electrical energy is stored in the capacitor, a charged capacitor can act as a source emf.
DISCHARGING
To DISCHARGE a capacitor, the charges on the two plates must be neutralized. This is accomplished by providing a conducting path between the two plates as shown in figure 43(B).
With the switch in position (4) the excess electrons on the negative plate can flow to the positive plate and neutralize its charge.
When the capacitor is discharged, the distorted orbits of the electrons in the dielectric return to their normal positions, and the stored energy is returned to the circuit.
It is important for you to note that a capacitor does not consume power. The energy the capacitor draws from the source is recovered when the capacitor is discharged.
CHARGE AND DISCHARGE OF AN RC SERIES CIRCUIT
Ohm’s law states that the voltage across a resistance is equal to the current through the resistance times the value of the resistance.
This means that a voltage is developed across a resistance, ONLY WHEN CURRENT FLOWS through the resistance. A capacitor is capable of storing or holding a charge of electrons.
When uncharged, both plates of the capacitor contain essentially the same number of free electrons. When charged, one plate contains more free electrons than the other plate.
The difference in the number of electrons is a measure of the charge on the capacitor.
The accumulation of this charge builds up a voltage across the terminals of the capacitor, and the charge continues to increase until this voltage equals the applied voltage.
The charge in a capacitor is related to the capacitance and voltage as follows:
Q = CE
in which Q is the charge in coulombs, C the capacitance in farads, and E the emf across the capacitor in volts.
CHARGE CYCLE
A voltage divider containing resistance and capacitance is connected in a circuit by means of a switch, as shown at the top of figure 44. Such a series arrangement is called an RC series circuit.
In explaining the charge and discharge cycles of an RC series circuit, the time interval from time t0 (time zero, when the switch is first closed) to time t1 (time one, when the capacitor reaches full charge or discharge potential) will be used.
(Note that switches S1 and S2 move at the same time and can never both be closed at the same time.)
When switch S1 of the circuit in figure 9 is closed at t0, the source voltage (ES) is instantly felt across the entire circuit.
- Graph 44(A) of the figure shows an instantaneous rise at time t0 from zero to source voltage (ES = 6 volts). Total voltage can be measured across the circuit between points 1 & 2.
- Graph 44(B) represents the charging current in the capacitor (iC). At time t0, charging current is MAXIMUM.
As time elapses toward time t1, there is a continuous decrease in current flowing into the capacitor.
The decreasing flow is caused by the voltage buildup across the capacitor.
At time t1, current flowing in the capacitor stops. At this time, the capacitor has reached full charge and has stored maximum energy in its electrostatic field.
- Graph 44(C) represents the voltage drop (e) across the resistor (R).
The value of er is determined by the amount of current flowing through the resistor on its way to the capacitor.
At time t0 the current flowing to the capacitor is maximum.
Thus, the voltage drop across the resistor is maximum (E = IR).
As time progresses toward time t1, the current flowing to the capacitor steadily decreases and causes the voltage developed across the resistor (R) to steadily decrease.
When time t1 is reached, current flowing to the capacitor is stopped and the voltage developed across the resistor has decreased to zero.
You should remember that capacitance opposes a change in voltage.
This is shown by comparing graph (A) to graph (D).
In graph (A) the voltage changed instantly from 0 volts to 6 volts across the circuit, while the voltage developed across the capacitor in graph (D) took the entire time interval from time t0 to time t1 to reach 6 volts.
The reason for this is that in the first instant at time t0, maximum current flows through R, and the entire circuit voltage is dropped across the resistor.
The voltage impressed across the capacitor at t0 is zero volts.
As time progresses toward t1, the decreasing current causes progressively less voltage to be dropped across the resistor (R), and more voltage builds up across the capacitor (C).
At time t1, the voltage felt across the capacitor is equal to the source voltage (6 volts), and the voltage dropped across the resistor (R) is equal to zero.
This is the complete charge cycle of the capacitor.
As you may have noticed, the processes which take place in the time interval t0 to t1 in a series RC circuit are exactly opposite to those in a series LR circuit.
For your comparison, the important points of the charge cycle of RC and LR circuits are summarized in Table 1.
DISCHARGE CYCLE
In figure 10 at time t0, the capacitor is fully charged.
When S1 is open and S2 closes, the capacitor discharge cycle starts.
At the first instant, circuit voltage attempts to go from source potential (6 volts) to zero volts, as shown in graph (A). Remember, though, the capacitor during the charge cycle has stored energy in an electrostatic field.
Because S2 is closed at the same time S1 is open, the stored energy of the capacitor now has a path for current to flow.
At t0, discharge current (id) from the bottom plate of the capacitor through the resistor (R) to the top plate of the capacitor (C) is maximum.
As time progresses toward t1, the discharge current steadily decreases until at time t1 it reaches zero, as shown in graph (B)
The discharge causes a corresponding voltage drop across the resistor as shown in graph (C).
At time t0, the current through the resistor is maximum and the voltage drop (er) across the resistor is maximum.
As the current through the resistor decreases, the voltage drop across the resistor decreases until at t1 it has reached a value of zero.
Graph (D) shows the voltage across the capacitor (ec) during the discharge cycle.
At time t0 the voltage is maximum and as time progresses toward time t1, the energy stored in the capacitor is depleted.
At the same time the voltage across the resistor is decreasing, the voltage (e) across the capacitor is decreasing until at time t1 the voltage (ec) reaches zero.
By comparing graph (A) with graph (D) of figure 3-10, you can see the effect that capacitance has on a change in voltage.
If the circuit had not contained a capacitor, the voltage would have ceased at the instant S1 was opened at time t0.
Because the capacitor is in the circuit, voltage is applied to the circuit until the capacitor has discharged completely at t1.
The effect of capacitance has been to oppose this change in voltage
RC TIME CONSTANT
The time required to charge a capacitor to 63 percent (actually 63.2 percent) of full charge or to discharge it to 37 percent (actually 36.8 percent) of its initial voltage is known as the TIME CONSTANT (TC) of the circuit.
The charge and discharge curves of a capacitor are shown in figure 46.
Note that the charge curve is like the curve in figure 9, graph (D), and the discharge curve like the curve in figure 9, graph (B).
The value of the time constant in seconds is equal to the product of the circuit resistance in ohms and the circuit capacitance in farads.
The value of one time constant is expressed mathematically as t = RC.
Some forms of this formula used in calculating RC time constants are:
t (in seconds) = R (in ohms) x C (in farads)
t (in seconds) = R (in megohms) x C (in microfarads)
t (in microseconds) = R (in ohms) x C (in microfarads)
t (in microseconds) = R (in megohms) x C (in picofarads)
UNIVERSAL TIME CONSTANT CHART
Because the impressed voltage and the values of R and C or R and L in a circuit are usually known, a UNIVERSAL TIME CONSTANT CHART (figure 12) can be used to find the time constant of the circuit.
Curve A is a plot of both capacitor voltage during charge and inductor current during growth.
Curve B is a plot of both capacitor voltage during discharge and inductor current during decay.
The time scale (horizontal scale) is graduated in terms of the RC or L/R time constants so that the curves may be used for any value of R and C or L and R.
The voltage and current scales (vertical scales) are graduated in terms of percentage of the maximum voltage or current so that the curves may be used for any value of voltage or current.
If the time constant and the initial or final voltage for the circuit in question are known, the voltages across the various parts of the circuit can be obtained from the curves for any time after the switch is closed, either on charge or discharge. The same reasoning is true of the current in the circuit.
The following problem illustrates how the universal time constant chart may be used.
An RC circuit is to be designed in which a capacitor (C) must charge to 20 percent (0.20) of the maximum charging voltage in 100 microseconds (0.0001 second).
Because of other considerations, the resistor (R) must have a value of 20,000 ohms. What value of capacitance is needed?
Given: Percent of charge = 20% (.20)
T = 100 µs
R = 20,000Ω
Find: The capacitance of capacitor C.
Solution: Because the only values given are in units of time and resistance, a variation of the formula to find RC time is used:
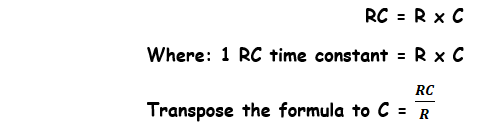
Find the value of RC by referring to the universal time constant chart in figure 12 and proceed as follows:
- Locate the 20 point on the vertical scale at the left side of the chart (percentage).
- Follow the horizontal line from this point to intersect curve A.
- Follow an imaginary vertical line from the point of intersection on curve A downward to cross the RC scale at the bottom of the chart.
Note: that the vertical line crosses the horizontal scale at about .22 RC as illustrated below:
The value selected from the graph means that a capacitor (including the one you are solving for) will reach twenty percent of full charge in twenty-two one-hundredths (.22) of one RC time constant.
Remember that it takes 100 μs for the capacitor to reach 20% of full charge.
Since 100 μs is equal to .22 RC (twenty-two one-hundredths), then the time required to reach one RC time constant must be equal to:
Now use the following formula to find C:
To summarize the previous procedures, the problem and solution are shown below without the step-by-step explanation.
Given: Percent of charge = 20% (.20)
t = 100 µs
R = 20,000Ω
Transpose the RC time constant formula as follows:
Find: RC
Substitute the R and RC values into the formula:
NOTE: The graphs shown in figures 11 & 12 are not entirely complete.
That is, the charge or discharge (or the growth or decay) is not quite complete in 5 RC or 5 L/R time constants.
However, when the values reach 0.99 of the maximum (corresponding to 5 RC or 5 L/R), the graphs may be considered accurate enough for all practical purposes.
CAPACITORS IN SERIES
The overall effect of connecting capacitors in series is to move the plates of the capacitors further apart. This is shown in figure 48.
Notice that the junction between C1 and C2 has both a negative and a positive charge. This causes the junction to be essentially neutral.
The total capacitance of the circuit is developed between the left plate of C1 and the right plate of C2. Because these plates are farther apart, the total value of the capacitance in the circuit is decreased.
Solving for the total capacitance (CT) of capacitors connected in series is similar to solving for the total resistance (RT) of resistors connected in parallel.
Note the similarity between the formulas for RT and CT:
If the circuit contains more than two capacitors, use the above formula. If the circuit contains only two capacitors, use the below formula:
Note: All values for CT, C1, C2, C3… Cn should be in farads.
It should be evident from the above formulas that the total capacitance of capacitors in series is less than the capacitance of any of the individual capacitors.
Example: Determine the total capacitance of a series circuit containing three capacitors whose values are 0.01 μF, 0.25 μF, and 50,000 pF, respectively.
Given:
C1 = 0.01 µs
C2 = 0.25 µs
C3 = 50.000 pF
The total capacitance of 0.008μF is slightly smaller than the smallest capacitor (0.01μF).
CAPACITORS IN PARALLEL
When capacitors are connected in parallel, one plate of each capacitor is connected directly to one terminal of the source, while the other plate of each capacitor is connected to the other terminal of the source.
Figure 49 shows all the negative plates of the capacitors connected together, and all the positive plates connected together.
CT, therefore, appears as a capacitor with a plate area equal to the sum of all the individual plate areas.
As previously mentioned, capacitance is a direct function of plate area. Connecting capacitors in parallel effectively increases plate area and thereby increases total capacitance.
For capacitors connected in parallel, the total capacitance is the sum of all the individual capacitances. The total capacitance of the circuit may be calculated using the formula:
CT = C1 + C2 + C3 + ……CN
where all capacitances are in the same units.
Example: Determine the total capacitance in a parallel capacitive circuit containing three capacitors whose values are 0.03 μF, 2.0 μF, and 0.25 μF, respectively.
Given:
C1 = 0.03 µF
C2 = 2 µF
C3 = 0.25 µF
Solution:
CT = C1 + C2 + C3
CT = 0.03 µF + 2.0 µF + 0.25 µF
CT = 2.28 µF
FIXED CAPACITOR
A fixed capacitor is constructed in such a manner that it possesses a fixed value of capacitance which cannot be adjusted.
A fixed capacitor is classified according to the type of material used as its dielectric, such as paper, oil, mica, or electrolyte.
Most types of capacitors include a dielectric spacer, which increases their capacitance. These dielectrics are most often insulators.
However, low capacitance devices are available with a vacuum between their plates, which allows extremely high voltage operation and low losses.
Variable capacitors with their plates open to the atmosphere were commonly used in radio tuning circuits. Later designs use polymer foil dielectric between the moving and stationary plates, with no significant air space between them.
In order to maximize the charge that a capacitor can hold, the dielectric material needs to have as high a permittivity as possible, while also having as high a breakdown voltage as possible.
Several solid dielectrics are available, including paper, plastic, glass, mica, and ceramic materials.
Paper was used extensively in older devices and offers relatively high voltage performance. However, it is susceptible to water absorption and has been largely replaced by plastic film capacitors.
Plastics offer better stability and aging performance, which makes them useful in timer circuits, although they may be limited to low operating temperatures and frequencies.
Ceramic capacitors are generally small, cheap, and useful for high-frequency applications, although their capacitance varies strongly with voltage and they age poorly.
They are broadly categorized as class 1 dielectrics, which have predictable variations of capacitance with temperature, or class 2 dielectrics, which can operate at higher voltage.
Glass and mica capacitors are extremely reliable, stable, and tolerant to high temperatures and voltages.
Electrolytic capacitors and supercapacitors are used to store small and larger amounts of energy, respectively, ceramic capacitors are often used in resonators, and parasitic capacitance occurs in circuits wherever the simple conductor-insulator-conductor structure is formed unintentionally by the configuration of the circuit layout.
Electrolytic capacitors use an aluminum or tantalum plate with an oxide dielectric layer. The second electrode is a liquid electrolyte, connected to the circuit by another foil plate.
Electrolytic capacitors offer very high capacitance but suffer from poor tolerances, high instability, gradual loss of capacitance especially when subjected to heat, and high leakage current.
Poor quality capacitors may leak electrolyte, which is harmful to printed circuit boards.
The conductivity of the electrolyte drops at low temperatures, which increases equivalent series resistance.
While widely used for power-supply conditioning, poor high-frequency characteristics make them unsuitable for many applications.
Electrolytic capacitors will self-degrade if unused for a period (around a year), and when full power is applied may short circuit, permanently damaging the capacitor and usually blowing a fuse or causing arcing in rectifier tubes.
They can be restored before use (and damage) by gradually applying the operating voltage, often done on antique vacuum tube equipment over a period of 30 minutes by using a variable transformer to supply AC power.
Unfortunately, the use of this technique may be less satisfactory for some solid-state equipment, which may be damaged by operation below its normal power range, requiring that the power supply first be isolated from the consuming circuits.
Such remedies may not be applicable to modern high-frequency power supplies as these produce full output voltage even with reduced input.
Supercapacitors: store large amounts of energy.
Supercapacitors made from carbon aerogel, carbon nanotubes, or highly porous electrode materials, offer extremely high capacitance (up to 5 kF as of 2010) and can be used in some applications instead of rechargeable batteries.
Alternating current capacitors are specifically designed to work online (mains) voltage AC power circuits.
They are commonly used in electric motor circuits and are often designed to handle large currents, so they tend to be physically large.
They are usually ruggedly packaged, often in metal cases that can be easily grounded/earthed. They also are designed with direct current breakdown voltages of at least five times the maximum AC voltage.
A PAPER CAPACITOR is made of flat thin strips of metal foil conductors that are separated by waxed paper (the dielectric material).
Paper capacitors usually range in value from about 300 picofarads to about 4 microfarads. The working voltage of a paper capacitor rarely exceeds 600 volts.
Paper capacitors are sealed with wax to prevent the harmful effects of moisture and to prevent corrosion and leakage. Many different kinds of outer covering are used on paper capacitors, the simplest being a tubular cardboard covering.
Some types of paper capacitors are encased in very hard plastic. These types are very rugged and can be used over a much wider temperature range than can the tubular cardboard type.
Figure 50(A) shows the construction of a tubular paper capacitor; part 50(B) shows a completed cardboard encased capacitor.
* This type of capacitor is considered obsolete but is included in this lesson for your information)
MICA CAPACITOR is made of metal foil plates that are separated by sheets of mica (the dielectric).
The whole assembly is encased in molded plastic. Figure 51(A) shows a cut-away view of a mica capacitor.
Because the capacitor parts are molded into a plastic case, corrosion and damage to the plates and dielectric are prevented. In addition, the molded plastic case makes the capacitor mechanically stronger.
Various types of terminals are used on mica capacitors to connect them into circuits.
These terminals are also molded into the plastic case.
Mica is an excellent dielectric and can withstand a higher voltage than can a paper dielectric of the same thickness. Common values of mica capacitors range from approximately 50 picofarads to 0.02 microfarad.
Some different shapes of mica capacitors are shown in figure 51(B).
A CERAMIC CAPACITOR is a fixed value capacitor with the ceramic material acting as the dielectric.
It is constructed of two or more alternating layers of ceramic and a metal layer acting as the electrodes.
The composition of the ceramic material defines the electrical behavior and therefore the application of the capacitors, which are divided into two stability classes:
- Class 1 ceramic capacitors with high stability and low losses for resonant circuit application.
- Class 2 ceramic capacitors with high volumetric efficiency for buffer, by-pass, and coupling applications.
Ceramic capacitors, especially the multilayer version (MLCC), are the most produced and used capacitors in electronic equipment with a produced quantity of approximately 1000 billion pieces per year.
Ceramic capacitors of special shapes and styles are used as capacitors for RFI/EMI suppression, as feed-through capacitors, and in larger dimensions as power capacitors for transmitters.
FILM CAPACITOR’s or plastic film capacitors are non-polarized capacitors with an insulating plastic film as the dielectric.
The dielectric films are drawn to a thin layer, provided with metallic electrodes, and wound into a cylindrical winding.
The electrodes of film capacitors may be metalized aluminum or zinc, applied on one or both sides of the plastic film, resulting in metalized film capacitors or a separate metallic foil overlying the film, called film/foil capacitors.
Metalized film capacitors offer self-healing properties. Dielectric breakdowns or shorts between the electrodes do not destroy the component.
The metalized construction makes it possible to produce wound capacitors with larger capacitance values (up to 100 µF and larger) in smaller cases than within film/foil construction.
Film/foil capacitors or metal foil capacitors use two plastic films as the dielectric. Each film is covered with a thin metal foil, mostly aluminum, to form the electrodes.
The advantage of this construction is the ease of connecting the metal foil electrodes, along with an excellent current pulse strength.
A key advantage of every film capacitor’s internal construction is direct contact to the electrodes on both ends of the winding. This contact keeps all current paths very short.
The design behaves like a large number of individual capacitors connected in parallel, thus reducing the internal ohmic losses (ESR) and parasitic inductance (ESL).
The inherent geometry of film capacitor structure results in low ohmic losses and a low parasitic inductance, which makes them suitable for applications with high surge currents (snubbers) and for AC power applications, or for applications at higher frequencies.
The plastic films used as the dielectric for film capacitors are Polypropylene (PP), Polyester (PET), Polyphenylene sulfide (PPS), Polyethylene naphthalate (PEN), and Polytetrafluoroethylene or Teflon (PTFE).
Polypropylene film material with a market share of something about 50% and Polyester film with something about 40% are the most used film materials.
The rest of something about 10% will be used by all other materials including PPS and paper with roughly 3%, each.
One of the great advantages of plastic films for capacitor fabrication is that plastic films have considerably fewer defects than paper sheets used in paper capacitors.
This allows the manufacture of plastic film capacitors with only a single layer of plastic film, whereas paper capacitors need a double layer of paper.
Plastic film capacitors were therefore significantly smaller in physical size (better volumetric efficiency), with the same capacitance value and the same dielectric strength as comparable paper capacitors.
Then-new plastic materials also showed further advantages compared with paper.
For example, lower hygroscopic characteristics of plastics allowed the housing of the capacitors to be made from new, inexpensive plastics instead of more-expensive metal cans.
Additionally, most plastics evidence fewer chemical changes during long-term use, thus offering excellent long-term stability of their electrical parameters.
Since around 1980 paper capacitors and metalized paper capacitors (MP capacitors) have almost completely been replaced by PET film capacitors, for most low-power DC electronic applications.
Paper is now used only in RFI suppression or motor run capacitors, or as a mixed dielectric combined with polypropylene films in large AC and DC capacitors for high power applications.
An ELECTROLYTIC CAPACITOR can be used where a large amount of capacitance is required.
As the name implies, an electrolytic capacitor contains an electrolyte.
This electrolyte can be in the form of a liquid (wet electrolytic capacitor).
The wet electrolytic capacitor is no longer in popular use due to the care needed to prevent the spilling of the electrolyte.
A dry electrolytic capacitor consists essentially of two metal plates separated by the electrolyte.
In most cases, the capacitor is housed in a cylindrical aluminum container which acts as the negative terminal of the capacitor (see figure 52).
The positive terminal (or terminals if the capacitor is of the multi-section type) is a lug (or lugs) on the bottom end of the container.
The capacitance value(s) and the voltage rating of the capacitor are generally printed on the side of the aluminum case.
Most electrolytic capacitors are polarized; hence, they can only be operated with a lower voltage on the terminal marked “-” without damaging the capacitor.
This generally limits electrolytic capacitors to supply-decoupling and bias-decoupling, since signal coupling usually involves both positive and negative voltages across the capacitor.
The large capacitance of electrolytic capacitors makes them particularly suitable for passing or bypassing low-frequency signals and storing large amounts of energy.
They are widely used in power supplies and for decoupling unwanted AC components from DC power connections.
Electrolytic capacitors range downwards from tens (exceptionally hundreds) of thousands of microfarads to about 100 nanofarads—smaller sizes are possible but have no advantage over other types.
Other types of capacitors are available in sizes typically up to about ten microfarads, but the larger sizes are much larger and more expensive than electrolytics (film capacitors of up to thousands of microfarads are available, but at very high prices).
Electrolytic capacitors are available with working voltages up to about 500V, although the highest capacitance values are not available at high voltage.
Working temperature is commonly 85°C for standard use and 105° for high-temperature use; higher temperature units are available but uncommon.
Unlike other types of capacitor, most electrolytic capacitors require that the voltage applied to one terminal (the anode) never become negative relative to the other (they are said to be “polarized”), so cannot be used with AC signals without a DC polarizing bias (non-polarized electrolytic capacitors are available for special purposes).
Leakage current, capacitance tolerance and stability, equivalent series resistance (ESR), and dissipation factor are significantly inferior to other types of capacitors, and working life is shorter.
Capacitors can lose capacitance as they age and lose electrolyte, particularly at high temperatures.
A common failure mode which causes difficult-to-find circuit malfunction is progressively increasing ESR without change of capacitance, again, particularly at high temperatures.
Large ripple currents flowing through the ESR generate harmful heat.
Two types of electrolytic capacitors are in common use: aluminum and tantalum.
Tantalum capacitors have generally better performance, higher price, and are available only in a more restricted range of parameters.
Solid polymer dielectric aluminum electrolytic capacitors have better characteristics than wet-electrolyte types—in particular lower and more stable ESR and longer life—at higher prices and more restricted values.
The type of dielectric used and its thickness govern the amount of voltage that can safely be applied to the electrolytic capacitor.
If the voltage applied to the capacitor is high enough to cause the atoms of the dielectric material to become ionized, arcing between the plates will occur.
In most other types of capacitors, arcing will destroy the capacitor. However, an electrolytic capacitor has the ability to be self-healing.
If the arcing is small, the electrolytic will regenerate itself. If the arcing is too large, the capacitor will not self-heal and will become defective.
Supercapacitors
Supercapacitors are a type of electrochemical capacitor, also called ultracapacitors.
The name is a generic term for electric double-layer capacitors (EDLC), pseudocapacitors, and hybrid capacitors.
Supercapacitors do not have a conventional solid dielectric. Supercapacitors are divided into three families, based on electrode design:
- Double-layer capacitors – with carbon electrodes or derivates with much higher electrostatic double-layer capacitance than electrochemical pseudocapacitance.
- Pseudocapacitors – with metal oxide or conducting polymer electrodes with a high amount of electrochemical pseudocapacitance.
- Hybrid capacitors – capacitors with asymmetric electrodes, one of which exhibits mostly electrostatic and the other mostly electrochemical capacitance, such as lithium-ion capacitors
Double-layer capacitance
Double-layer capacitance store electrical energy by means of an electrical double layer effect (EDL effect).
Unlike a ceramic capacitor or aluminum electrolytic capacitor, the Electrical Double Layer Capacitor (EDLC) contains no conventional dielectric. Instead, an electrolyte (solid or liquid) is filled between two electrodes.
In EDLC, an electrical condition called “electrical double layer” which is formed between the electrodes and electrolyte works as the dielectric.
Capacitance is proportional to the surface area of the electrical double layer. Therefore using activated carbon which has a large surface area for electrodes, enables EDLC to have high capacitance.
The mechanism of ion absorption and desorption to the electrical double layer contributes to charge and discharge of EDLC.
By applying voltage to the facing electrodes, ions are drawn to the surface of the electrical double layer and EDLC is charged. Conversely, they move away when discharging EDLC.
This is how EDLC is charged and discharged.
This electrical phenomenon appears at the interface between a metallic conductive electrode and an adjacent liquid electrolyte in a supercapacitor.
Along this boundary between two different phases, two layers of ions with opposite polarity will arise if a voltage is applied.
These two layers of ions are separated by a single layer of solvent molecules adhere at the surface of the electrode serves like a dielectric in a conventional capacitor.
The amount of electric charge stored in a double-layer capacitance is linearly proportional to the applied voltage and depends primarily on the electrode surface.
The unit of double-layer capacitance is farad.
Storage is achieved by separation of charge in a Helmholtz double layer at the interface between the surface of a conductor and an electrolytic solution.
Pseudocapacitance
Storage is achieved by redox reactions, electrosorption, or intercalation on the surface of the electrode or by specifically adsorpted ions that result in a reversible faradaic charge transfer.
The pseudocapacitance is faradaic in origin.
Double-layer capacitance and pseudocapacitance each contribute to the total capacitance value of a supercapacitor.
The ratio of the two depends on the design of the electrodes and the composition of the electrolyte.
Pseudocapacitance can increase capacitance by as much as an order of magnitude.
A pseudocapacitor is part of an electrochemical capacitor and forms together with an electric double-layer capacitor (EDLC) to create a supercapacitor.
A pseudocapacitor has a chemical reaction at the electrode, unlike EDLCs where the electrical charge storage is stored electrostatically with no interaction between the electrode and the ions.
An example is a redox reaction where the ion is O2+ and during charging, one electrode hosts a reduction reaction and the other an oxidation reaction.
Under discharge, the reactions are reversed.
Unlike batteries, in faradaic electron charge-transfer ions simply cling to the atomic structure of an electrode.
This faradaic energy storage with only fast redox reactions makes charging and discharging much faster than batteries.
Double-layer capacitance and pseudocapacitance combine to produce a Supercapacitors capacitance value.
Pseudocapacitance may be higher by a factor of 100 than double-layer capacitance with the same electrode surface.
TYPES OF SUPERCAPACITORS
Supercapacitors are divided into three families, according to the relative amounts of capacitance in the double layers vs pseudocapacitance:
- Double-layer capacitors – Electrochemical capacitors in which the static double-layer capacitance is significantly higher than the faradaic pseudocapacitance use activated carbon or derivate, carbon aerogels, carbide-derived carbons, or carbon nanotubes as electrode material
- Pseudocapacitors – Electrochemical capacitors in which the faradaic pseudocapacitance is significantly higher than the static double-layer capacitance use conductive polymer or transition metal oxides with faradaic charge transfer as electrode material
- Hybrid capacitors – Capacitors with asymmetric electrodes exhibit significant high value of double-layer capacitance on one electrode as well as significant high value of pseudocapacitance on the other, coupling a double-layer electrode with a second pseudocapacitance or composite electrode, e.g. lithium-ion capacitors.
Supercapacitors have the highest capacitance values per unit volume and have the greatest energy density of all capacitors, reaching 12,000 F/1.2 V, with capacitance values up to 10,000 times that of electrolytic capacitors.
Supercapacitors are closing the gap between capacitors and batteries.
In terms of specific energy and specific power, this gap covered several orders of magnitude.
- Supercapacitors have reduced this gap to a single order of magnitude, offering about 10% of the capacity of batteries.
- Supercapacitor power density is generally 10 to 100 times greater than batteries.
- Power density combines the energy density with the speed at which the energy can be delivered to the load.
Unlike batteries, in the faradaic redox reactions, the ions cling to the atomic structure of an electrode, and no or negligibly small chemical modifications are involved in charge/discharge.
This energy storage with fast charge transfer makes charging and discharging much faster than batteries.
Additionally, supercapacitors better tolerate repeated rapid charge and discharge cycles.
This makes them well-suited for parallel connection with batteries and may improve battery performance in terms of power density.
The electrolyte connects the two electrodes.
This distinguishes electrochemical from electrolytic capacitors, in which the electrolyte is also the cathode, and thus forms the second electrode.
Supercapacitors are polarized and may be operated only with the correct polarity.
The polarity is controlled by design with asymmetric electrodes, or by a voltage applied during manufacture for those with symmetric electrodes.
Supercapacitors support varied applications, including:
- Long, small currents for static memory (SRAM) in electronic equipment.
- Power electronics that require brief, high currents as in the KERS system in Formula 1 cars, for electrical energy storage/delivery
- Regenerative braking in vehicles such as buses and trains
Supercapacitors are rarely interchangeable, especially those with higher energy densities.
IEC standard 62391-1 Fixed electric double layer capacitors for use in electronic equipment identifies four application classes:
Class 1, Memory backup, discharge current in mA = 1 • C (F)
Class 2, Energy storage, discharge current in mA = 0.4 • C (F) • V (V)
Class 3, Power, discharge current in mA = 4 • C (F) • V (V)
Class 4, Instantaneous power, discharge current in mA = 40 • C (F) • V (V)
VARIABLE CAPACITOR
A variable capacitor is a capacitor whose capacitance may be intentionally and repeatedly changed mechanically or electronically.
Variable capacitors are often used in L/C circuits to set the resonance frequency, e.g. to tune a radio (therefore they are sometimes called tuning capacitors), or as a variable reactance, e.g. for impedance matching in antenna tuners.
Generally, two versions of variable capacitors have to be distinguished
- Tuning capacitor – variable capacitor for intentionally and repeatedly tuning an oscillator circuit in radio or another tuned circuits
- Trimmer capacitor – small variable capacitor usually for one-time oscillator circuit internal adjustment
A typical variable capacitor (adjustable capacitor) is the rotor-stator type. It consists of two sets of metal plates arranged so that the rotor plates move between the stator plates. Air is the dielectric.
As the position of the rotor is changed, the capacitance value is likewise changed. This type of capacitor is used for tuning most radio receivers. Its physical appearance and its symbol are shown in figure 53.
Another type of variable capacitor (trimmer capacitor) and its symbol is shown in figure 54.
A trimmer capacitor is an adjustable variable capacitor, they are common in precision circuitry like A/V components, and may need to be adjusted when the equipment is serviced.
Trimmer capacitors can be tuned within a certain range for their capacitance as per the specifications of the circuit.
These capacitors can also be termed analogous to presets in terms of the functions they perform.
Such variable capacitors find their application in filter tuning, small radios, car audio systems, and several such instruments.
The capacitance is usually adjusted by turning a screw.
Trimmer capacitors are only available with very small capacitances, normally less than 100pF.
It is impossible to reduce their capacitance to zero, so they are usually specified by their minimum and maximum values, for example, 2-10pF. Trimmer’s capacitors come in a variety of sizes and levels of precision.
Mechanical and Digital Variable Capacitors
In mechanically controlled variable capacitors, the distance between the plates, or the amount of plate surface area which overlaps, can be changed.
The most common form arranges a group of semicircular metal plates on a rotary axis (“rotor”) that are positioned in the gaps between a set of stationary plates (“stator”) so that the area of overlap can be changed by rotating the axis.
Air or plastic foils can be used as dielectric material.
By choosing the shape of the rotary plates, various functions of capacitance vs. angle can be created, e.g. to obtain a linear frequency scale.
Various forms of reduction gear mechanisms are often used to achieve finer tuning control, i.e. to spread the variation of capacity over a larger angle, often several turns.
A vacuum variable capacitor uses a set of plates made from concentric cylinders that can be slid in or out of an opposing set of cylinders (sleeve and plunger).
These plates are then sealed inside of a non-conductive envelope such as glass or ceramic and placed under a high vacuum.
The movable part (plunger) is mounted on a flexible metal membrane that seals and maintains the vacuum.
A screw shaft is attached to the plunger, when the shaft is turned the plunger moves in or out of the sleeve, and the value of the capacitor changes.
The vacuum not only increases the working voltage and current handling capacity of the capacitor it also greatly reduces the chance of arcing across the plates.
The most common usage for vacuum variables is in high-powered transmitters such as those used for broadcasting, military and amateur radio as well as high-powered RF tuning networks.
Vacuum variables can also be more convenient since the elements are under a vacuum the working voltage can be higher than an air variable the same size, allowing the size of the vacuum capacitor to be reduced.
Very cheap variable capacitors are constructed from layered aluminum and plastic foils that are variably pressed together using a screw.
These so-called squeezers can’t provide a stable and reproducible capacitance, however.
A variant of this structure that allows for linear movement of one set of plates to change the plate overlap area is also used and might be called a slider.
This has practical advantages for makeshift or home construction and may be found in resonant loop antennas or crystal radios.
Small variable capacitors operated by screwdriver (for instance, to precisely set a resonant frequency at the factory and then never be adjusted again) are called trimmer capacitors.
In addition to air and plastic, trimmers can also be made using a ceramic dielectric.
A Digitally tuned capacitor is an IC variable capacitor based on several technologies.
MEMS, BST, and SOI/SOS devices are available from a number of suppliers and vary in capacitance range, quality factor, and resolution for different RF tuning applications.
MEMS devices have the highest quality factor and are highly linear, and therefore are suitable for antenna aperture tuning, dynamic impedance matching, power amplifier load matching, and adjustable filters.
BST devices are based on Barium Strontium Titanate and vary the capacitance by applying high voltage to the device.
The tuning accuracy is limited only by the accuracy of the D-A converter circuitry that generates the high voltage.
The limitations for BST are stability over temperature and linearity in demanding applications.
SOI/SOS tuning devices are constructed as solid-state FET switches built on insulated CMOS wafers and use MIM caps arranged in binary-weighted values to achieve different capacitance values.
High voltage endurance requires multiple FET devices in series which adds series resistance and lowers the quality factor.
COLOR CODES FOR CAPACITORS
Generally, the actual values of Capacitance, Voltage or Tolerance are marked onto the body of the capacitors in the form of alphanumeric characters.
However, when the value of the capacitance is of a decimal value problems arise with the marking of a “Decimal Point” as it could easily not be noticed resulting in a misreading of the actual value.
Instead, letters such as p (pico) or n (nano) are used in place of the decimal point to identify its position and the weight of the number.
For example, a capacitor can be labeled as, n47 = 0.47nF, 4n7 = 4.7nF or 47n = 47nF and so on.
Also, sometimes capacitors are marked with the capital letter K to signify a value of one thousand pico-Farads, so for example, a capacitor with the markings of 100K would be 100 x 1000pF or 100nF.
To reduce the confusion regarding letters, numbers, and decimal points, an
The international color coding scheme was developed many years ago as a simple way of identifying capacitor values and tolerances.
It consists of colored bands (in spectral order) known commonly as the Capacitor Color Code system and whose meanings are illustrated below:
Although the capacitance value may be printed on the body of a capacitor, it may also be indicated by a color code. The Capacitor Color Code system was used for many years on unpolarised polyester and mica molded capacitors.
Capacitor Color Code Table
An example of the use of capacitor color codes is given as:
Capacitor Voltage Reference
- Type J- Dipped Tantalum Capacitors.
- Type K- Mica Capacitors.
- Type L- Polyester/Polystyrene Capacitors.
- Type M- Electrolytic 4 Band Capacitors
- Type N – Electrolytic 3 Band Capacitors.
This system of color coding is now obsolete but there are still many “old” capacitors around.
Capacitor Voltage Code Table
An example of the use of capacitor color codes is given as:
Metalized Polyester Capacitor
Currently, small capacitors such as film or disk types conform to the BS1852 Standard and its replacement, BS EN 60062, where the colors have been replaced by a letter or number coded system.
Generally, the code consists of 2 or 3 numbers and an optional tolerance letter code to identify the tolerance.
Where a two-number code is used the value of the capacitor only is given in picofarads, for example, 47 = 47 pF and 100 = 100pF etc.
A three-letter code consists of the two value digits and a multiplier much like the resistor color codes in the resistors section.
For example, the digits 471 = 47*10 = 470pF.
Three-digit codes are often accompanied by an additional tolerance letter code as given below.
Consider the capacitor below:
The capacitor on the left is a ceramic disc-type capacitor that has the code 473J printed onto its body.
Then the 4 = 1st digit, the 7 = 2nd digit, the 3 is the multiplier in pico-Farads, pF and the letter J is the tolerance and this translates to:
47pF * 1,000 (3 zero’s) = 47,000 pF, 47nF or 0.047 uF the J indicates a tolerance of +/- 5%
Then by just using numbers and letters as codes on the body of the capacitor, we can easily determine the value of its capacitance either in Pico-farad’s, Nano-farads or Micro-farads and a list of these “international” codes is given in the following table along with their equivalent capacitances.
Capacitor Tolerance Letter Codes Table
Capacitor Letter Codes Table
TYPES OF CAPACITORS—Capacitors are manufactured in various forms and may be divided into two main classes-fixed capacitors and variable capacitors.
A fixed capacitor is constructed to have a constant or fixed value of capacitance. A variable capacitor allows the capacitance to be varied or adjusted.
INDUCTIVE AND CAPACITIVE REACTANCE
You have already learned how inductance and capacitance individually behave in a direct current circuit.
In this lesson, you will be shown how inductance, capacitance, and resistance affect alternating current.
INDUCTANCE AND ALTERNATING CURRENT
This might be a good place to recall what you learned about phase.
When two things are in step, going through a cycle together, falling together, and rising together, they are in phase.
When they are out of phase, the angle of lead or lag-the number of electrical degrees by which one of the values leads or lags the other-is a measure of the amount they are out of step.
The time it takes the current in an inductor to build up to maximum and to fall to zero is important for another reason.
It helps illustrate a very useful characteristic of inductive circuits-the current through the inductor always lags the voltage across the inductor.
A circuit having pure resistance (if such a thing were possible) would have the alternating current through it and the voltage across it rising and falling together.
This is illustrated in figure 55(A), which shows the sine waves for current and voltage in a purely resistive circuit having an ac source.
The current and voltage do not have the same amplitude, but they are in phase.
In the case of a circuit having inductance, the opposing force of the counter emf would be enough to keep the current from remaining in phase with the applied voltage.
You learned that in a dc circuit containing pure inductance the current took time to rise to maximum even though the full applied voltage was immediately at maximum.
Figure 55(B) shows the waveforms for a purely inductive ac circuit in steps of quarter-cycles.
With an ac voltage, in the first quarter-cycle (0º to 90º ) the applied ac voltage is continually increasing.
If there was no inductance in the circuit, the current would also increase during this first quarter-cycle. You know this circuit does have inductance.
Since inductance opposes any change in current flow, no current flows during the first quarter-cycle.
In the next quarter-cycle (90º to 180º ) the voltage decreases back to zero; current begins to flow in the circuit and reaches a maximum value at the same instant the voltage reaches zero.
The applied voltage now begins to build up to maximum in the other direction, to be followed by the resulting current.
When the voltage again reaches its maximum at the end of the third quarter-cycle (270º ) all values are exactly opposite to what they were during the first half-cycle.
The applied voltage leads the resulting current by one quarter-cycle or 90 degrees.
To complete the full 360º cycle of the voltage, the voltage again decreases to zero and the current builds to a maximum value.
You must not get the idea that any of these values stops cold at a particular instant. Until the applied voltage is removed, both current and voltage are always changing in amplitude and direction.
As you know the sine wave can be compared to a circle.
Just as you mark off a circle into 360 degrees, you can mark off the time of one cycle of a sine wave into 360 electrical degrees.
This relationship is shown in figure 56. By referring to this figure you can see why the current is said to lag the voltage, in a purely inductive circuit, by 90 degrees.
Furthermore, by referring to figures 56 you can see why the current and voltage are said to be in phase in a purely resistive circuit.
In a circuit having both resistance and inductance then, as you would expect, the current lags the voltage by an amount somewhere between 0 and 90 degrees.
A simple memory aid to help you remember the relationship of voltage and current in an inductive circuit is the word ELI.
Since
E is the symbol for voltage,
L is the symbol for inductance, and
I is the symbol for current;
The word ELI demonstrates that current comes after (Lags) voltage in an inductor.
INDUCTIVE REACTANCE
The reduction of current flow in a circuit due to induction is called inductive reactance.
By taking a closer look at a coil of wire and applying Lenz’s law, it can be seen how inductance reduces the flow of current in the circuit.
When the current flowing through an inductor continuously reverses itself, as in the case of an ac source, the inertia effect of the cemf is greater than with dc.
The greater the amount of inductance (L), the greater the opposition from this inertia effect. Also, the faster the reversal of current, the greater this inertial opposition.
This opposing force which an inductor presents to the FLOW of alternating current cannot be called resistance, since it is not the result of friction within a conductor.
The name given to it is INDUCTIVE REACTANCE because it is the “reaction” of the inductor to the changing value of alternating current.
Inductive reactance is measured in ohms and its symbol is XL.
As you know, the induced voltage in a conductor is proportional to the rate at which magnetic lines of force cut the conductor.
The greater the rate (the higher the frequency), the greater the cemf.
Also, the induced voltage increases with an increase in inductance; the more ampere-turns, the greater the cemf.
Reactance, then, increases with an increase of frequency and with an increase of inductance.
The formula for inductive reactance is as follows:
XL = 2πfL
Where
XL is inductive reactance in ohms
2π is a constant in which the Greek letter π called “pi” represents 3.1416 and 2 X π = 6.28 approximately
F is frequency of the alternating current in henrys
L is inductance in henrys
The following example problem illustrates the computation of XL.
Given
f = 60 Hz
L = 20 H
Solution
XL = 2πfL
XL = 6.28 x 60 Hz x 20 H
XL = 7.536Ω
CAPACITORS AND ALTERNATING CURRENT
The four parts of figure 57 show the variation of the alternating voltage and current in a capacitive circuit, for each quarter of one cycle.
- The solid line represents the voltage across the capacitor, and the dotted line represents the current.
- The line running through the center is the zero, or reference point, for both the voltage and the current.
- The bottom line marks off the time of the cycle in terms of electrical degrees.
Assume that the ac voltage has been acting on the capacitor for some time before the time represented by the starting point of the sine wave in the figure.
At the beginning of the first quarter-cycle (0º to 90º), the voltage has just passed through zero and is increasing in the positive direction.
Since the zero point is the steepest part of the sine wave, the voltage is changing at its greatest rate.
The charge on a capacitor varies directly with the voltage, and therefore the charge on the capacitor is also changing at its greatest rate at the beginning of the first quarter-cycle.
In other words, the greatest numbers of electrons are moving off one plate and onto the other plate.
Thus the capacitor current is at its maximum value, as part (A) of the figure shows.
As the voltage proceeds toward maximum at 90 degrees, its rate of change becomes less and less, hence the current must decrease toward zero.
At 90 degrees the voltage across the capacitor is maximum, the capacitor is fully charged, and there is no further movement of electrons from plate to plate.
That is why the current at 90 degrees is zero.
At the end of this first quarter-cycle, the alternating voltage stops increasing in the positive direction and starts to decrease.
It is still a positive voltage, but to the capacitor, the decrease in voltage means that the plate which has just accumulated an excess of electrons must lose some electrons.
The current flow, therefore, must reverse its direction.
Part (B) of the figure shows the current curve to be below the zero line (negative current direction) during the second quarter-cycle (90º to 180º).
At 180 degrees the voltage has dropped to zero.
This means that for a brief instant the electrons are equally distributed between the two plates; the current is maximum because the rate of change of voltage is maximum.
Just after 180 degrees the voltage has reversed polarity and starts building up its maximum negative peak which is reached at the end of the third quarter-cycle (180º to 270º).
During this third quarter-cycle, the rate of voltage change gradually decreases as the charge builds to a maximum at 270 degrees.
At this point, the capacitor is fully charged and it carries the full impressed voltage.
Because the capacitor is fully charged there is no further exchange of electrons; therefore, the current flow is zero at this point. The conditions are exactly the same as at the end of the first quarter-cycle (90º) but the polarity is reversed.
Just after 270 degrees the impressed voltage once again starts to decrease, and the capacitor must lose electrons from the negative plate.
It must discharge, starting at a minimum rate of flow and rising to a maximum.
This discharging action continues through the last quarter-cycle (270º to 360º) until the impressed-voltage has reached zero.
At 360 degrees you are back at the beginning of the entire cycle, and everything starts over again.
If you examine the complete voltage and current curves in part D, you will see that the current always arrives at a certain point in the cycle 90 degrees ahead of the voltage, because of the charging and discharging action.
You know that this time and place relationship between the current and voltage is called the phase relationship.
The voltage-current phase relationship in a capacitive circuit is exactly the opposite of that in an inductive circuit. The current of a capacitor leads the voltage across the capacitor by 90 degrees.
You realize that the current and voltage are both going through their individual cycles at the same time during the period the ac voltage is impressed.
The current does not go through part of its cycle (charging or discharging), stop, and wait for the voltage to catch up. The amplitude and polarity of the voltage and the amplitude and direction of the current are continually changing.
Their positions with respect to each other and to the zero line at any electrical instant-any degree between zero and 360 degrees-can be seen by reading upwards from the time-degree line.
The current swing from the positive peak at zero degrees to the negative peak at 180 degrees is NOT a measure of the number of electrons, or the charge on the plates.
It is a picture of the direction and strength of the current in relation to the polarity and strength of the voltage appearing across the plates.
At times it is convenient to use the word “ICE” to remember the phase relationship of the current and voltage in capacitive circuits.
I is the symbol for current, and in the word ICE, it leads or comes before, the symbol for voltage, E. C, of course, stands for capacitor.
I is for current
C is for capacitor
E is for voltage
This memory aid is similar to the “ELI” used to remember the current and voltage relationship in an inductor.
The phrase “ELI the ICE man” is helpful in remembering the phase relationship in both the inductor and capacitor.
Since the plates of the capacitor are changing polarity at the same rate as the ac voltage, the capacitor seems to pass an alternating current.
Actually, the electrons do not pass through the dielectric, but their rushing back and forth from plate to plate causes a current flow in the circuit.
It is convenient, however, to say that the alternating current flows “through” the capacitor.
You know this is not true, but the expression avoids a lot of trouble when speaking of current flow in a circuit containing a capacitor.
By the same shortcut, you may say that the capacitor does not pass a direct current (if both plates are connected to a dc source, current will flow only long enough to charge the capacitor).
With a capacitor type of hookup in a circuit containing both ac and dc, only the ac will be “passed” on to another circuit.
You have now learned two things to remember about a capacitor:
- A capacitor will appear to conduct an alternating current and
- A capacitor will not conduct a direct current.
CAPACITIVE REACTANCE
So far you have been dealing with the capacitor as a device which passes ac and in which the only opposition to the alternating current has been the normal circuit resistance present in any conductor.
However, capacitors themselves offer very real opposition to current flow.
This opposition arises from the fact that, at a given voltage and frequency, the number of electrons that go back and forth from plate to plate is limited by the storage ability-that is the capacitance of the capacitor.
As the capacitance is increased, a greater number of electrons change plates every cycle, and (since current is a measure of the number of electrons passing a given point in a given time) the current is increased.
Increasing the frequency will also decrease the opposition offered by a capacitor.
This occurs because the number of electrons which the capacitor is capable of handling at a given voltage will change plates more often.
As a result, more electrons will pass a given point in a given time (greater current flow).
The opposition which a capacitor offers to ac is therefore inversely proportional to frequency and to capacitance.
This opposition is called CAPACITIVE REACTANCE.
You may say that capacitive reactance decreases with increasing frequency or, for a given frequency, the capacitive reactance decreases with increasing capacitance.
The symbol for capacitive reactance is XC.
Now you can understand why it is said that the XC varies inversely with the product of the frequency and capacitance.
The following example problem illustrates the computation of XC.
Given:
f = 100 Hz
C = 50 µF
Solution:
REACTANCE, IMPEDANCE, AND POWER RELATIONSHIPS IN AC CIRCUITS
Up to this point, inductance and capacitance have been explained individually in ac circuits.
The rest of this chapter will concern the combination of inductance, capacitance, and resistance in ac circuits.
To explain the various properties that exist within ac circuits, the series RLC circuit will be used,
Figure 58 is the schematic diagram of the series RLC circuit.
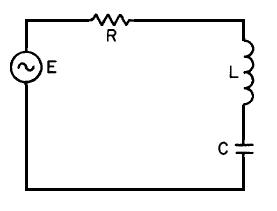
The symbol shown in figure 4, marked E, is the general symbol used to indicate an ac voltage source.
REACTANCE
The effect of inductive reactance is to cause the current to lag the voltage, while that of capacitive reactance is to cause the current to lead the voltage.
Therefore, since inductive reactance and capacitive reactance are exactly opposite in their effects, what will be the result when the two are combined?
It is not hard to see that the net effect is a tendency to cancel each other, with the combined effect then equal to the difference between their values.
This resultant is called REACTANCE; it is represented by the symbol X and expressed by the equation.
X = XL – XC or X = XC – XL.
Thus, if a circuit contains 50 ohms of inductive reactance and 25 ohms of capacitive reactance in series, the net reactance, or X, is 50 ohms – 25 ohms, or 25 ohms of inductive reactance.
For a practical example, suppose you have a circuit containing an inductor of 100 μH in series with a capacitor of .001 μF and operating at a frequency of 4 MHz.
What is the value of net reactance or X?
Given:
F = 4MHz
L = 100 µH
C = .001 µF
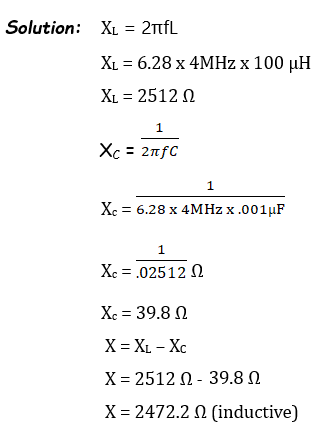
Now assume you have a circuit containing a 100 – μH inductor in series with a .0002-μF capacitor and operating at a frequency of 1 MHz.
What is the value of the resultant reactance in this case?
Given:
f = 1MHz
L = 100 µH
C = .0002 µF
You will notice that in this case, the inductive reactance is smaller than the capacitive reactance and is therefore subtracted from the capacitive reactance.
These two examples serve to illustrate an important point: when capacitive and inductive reactances are combined in series, the smaller is always subtracted from the larger, and the resultant reactance always takes the characteristics of the larger.
IMPEDANCE
From your study of inductance and capacitance, you know how inductive reactance and capacitive reactance act to oppose the flow of current in an ac circuit. However, there is another factor, the resistance, which also opposes the flow of the current.
Since, in practice, ac circuits containing reactance also contain resistance, the two combine to oppose the flow of current. This combined opposition by the resistance and the reactance is called the IMPEDANCE and is represented by the symbol Z.
Since the values of resistance and reactance are both given in ohms, it might at first seem possible to determine the value of the impedance by simply adding them together. It cannot be done so easily, however. You know that in an ac circuit which contains only resistance, the current and the voltage will be in step (that is, in-phase) and will reach their maximum values at the same instant.
You also know that in an ac circuit containing only reactance, the current will either lead or lag the voltage by one-quarter of a cycle or 90 degrees. Therefore, the voltage in a purely reactive circuit will differ in phase by 90 degrees from that in a purely resistive circuit, and for this reason, reactance and resistance are rot combined by simply adding them.
When reactance and resistance are combined, the value of the impedance will be greater than either.
It is also true that the current will not be in step with the voltage, nor will it differ in phase by exactly 90 degrees from the voltage, but it will be somewhere between the in-step and the 90-degree out-of-step conditions. The larger the reactance compared with the resistance, the more nearly the phase difference will approach 90º.
The larger the resistance compared to the reactance, the more the phase difference will approach zero degrees. If the value of resistance and reactance cannot simply be added together to find the impedance or Z, how is it determined?
Because the current through a resistor is in step with the voltage across it and the current in a reactance differs by 90 degrees from the voltage across it, the two are at right angles to each other. They can therefore be combined by means of the same method used in the construction of a right-angle triangle.
Assume you want to find the impedance of a series combination of 8 ohms resistance and 5 ohms inductive reactance.
Start by drawing a horizontal line, R, representing 8 ohms resistance, as the base of the triangle. Then, since the effect of the reactance is always at right angles, or 90 degrees, to that of the resistance, draw the line XL, representing 5 ohms inductive reactance, as the altitude of the triangle.
This is shown in figure 59. Now, complete the hypotenuse (longest side) of the triangle the hypotenuse represents the impedance of the circuit.
One of the properties of a right triangle is:
(hypotenuse)2 = (base)2 + (altitude)2
or
Applied to impedance this becomes (impedance)2 = (resistance)2 + (reactance)2
or
or
Now suppose you apply this equation to check your results in the example given above.
When you have a capacitive reactance to deal with instead of inductive reactance, as in the previous example, it is customary to draw the line representing the capacitive reactance in a downward direction.
This is shown in figure 59.
The line is drawn downward for capacitive reactance to indicate that it acts in a direction opposite to inductive reactance, which is drawn upward.
In a series circuit containing capacitive reactance, the equation for finding the impedance becomes:
In many series circuits, you will find resistance combined with both inductive reactance and capacitive reactance.
Since you know that the value of the reactance, X, is equal to the difference between the values of the inductive reactance, XL, and the capacitive reactance, XC, the equation for the impedance in a series circuit containing R, XL, and XC then becomes:
NOTE: the formulas on this page can be used to calculate Z only if the resistance and reactance are connected in series.
In figure 61, you will see the method which may be used to determine the impedance in a series circuit consisting of resistance, inductance, and capacitance.
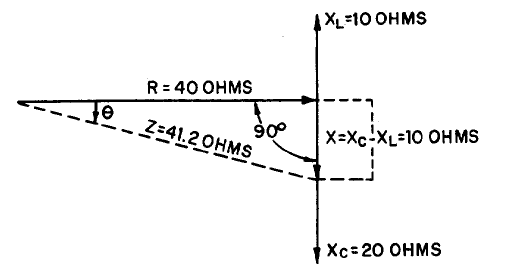
Assume that 10 ohms inductive reactance and 20 ohms capacitive reactance are connected in series with 40 ohms resistance.
Let the horizontal line represent the resistance R. The line drawn upward from the end of R represents the inductive reactance, XL.
Represent the capacitive reactance by a line drawn downward at right angles from the same end of R. The resultant of XL and XC is found by subtracting XL from XC.
This resultant represents the value of X.
Thus:
X = XC – XL
X = 10 ohms
The line, Z, will then represent the results of R and X. The value of Z can be calculated as follows:
Given:
XL = 10Ω
XC = 20Ω
R = 40Ω
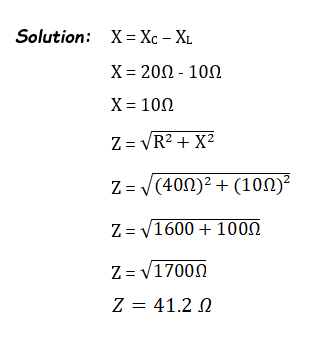
OHMS LAW FOR AC
In general, Ohm’s law cannot be applied to alternating-current circuits since it does not consider the reactance which is always present in such circuits.
However, by a modification of Ohm’s law which does take into consideration the effect of reactance, we obtain a general law which is applicable to ac circuits.
Because the impedance, Z, represents the combined opposition of all the reactances and resistances, this general law for ac is;
This general modification applies to alternating current flowing in any circuit, and any one of the values may be found from the equation if the others are known.
For example, suppose a series circuit contains an inductor having 5 ohms resistance and 25 ohms inductive reactance in series with a capacitor having 15 ohms capacitive reactance.
If the voltage is 50 volts, what is the current?
Now suppose the circuit contains an inductor having 5 ohms resistance and 15 ohms inductive reactance in series, with a capacitor having 10 ohms capacitive reactance. If the current is 5 amperes, what is the voltage?
POWER IN AC CIRCUITS
You know that in a direct current circuit, the power is equal to the voltage times the current, or P = E × I. If a voltage of 100 volts applied to a circuit produces a current of 10 amperes, the power is 1000 watts.
This is also true in an ac circuit when the current and voltage are in phase; that is when the circuit is effectively resistive. But, if the ac circuit contains reactance, the current will lead or lag the voltage by a certain amount (the phase angle).
When the current is out of phase with the voltage, the power indicated by the product of the applied voltage and the total current gives only what is known as the APPARENT POWER.
The TRUE POWER depends upon the phase angle between the current and voltage. The symbol for phase angle is Θ (Theta). When an alternating voltage is impressed across a capacitor, power is taken from the source and stored in the capacitor as the voltage increases from zero to its maximum value. Then, as the impressed voltage decreases from its maximum value to zero, the capacitor discharges and returns the power to the source.
Likewise, as the current through an inductor increases from its zero value to its maximum value, the field around the inductor builds up to a maximum. When the current decreases from maximum to zero, the field collapses and returns the power to the source.
You can see, therefore, that no power is used up in either case since the power alternately flows to and from the source. This power that is returned to the source by the reactive components in the circuit is called REACTIVE POWER.
In a purely resistive circuit, all of the power is consumed, and none is returned to the source; in a purely reactive circuit, no power is consumed, and all of the power is returned to the source. It follows that in a circuit that contains both resistance and reactance, there must be some power dissipated in the resistance as well as some returned to the source by the reactance. In figure 62, you can see the relationship between the voltage, the current, and the power in such a circuit.
The part of the power curve shown below the horizontal reference line is the result of multiplying a positive instantaneous value of current by a negative instantaneous value of the voltage, or vice versa.
As you know, the product obtained by multiplying a positive value by a negative value will be negative.
Therefore the power at that instant must be considered as negative power. In other words, during this time, the reactance was returning power to the source.
The instantaneous power in the circuit is equal to the product of the applied voltage and current through the circuit.
When the voltage and current are of the same polarity, they are acting together and taking power from the source.
When the polarities are unlike, they are acting in opposition, and power is being returned to the source.
Briefly then, in an ac circuit that contains reactance and resistance, the apparent power is reduced by the power returned to the source so that in such a circuit, the net power, or true power, is always less than the apparent power.
As mentioned before, the true power of a circuit is the power used in the circuit. This power, measured in watts, is the power associated with the total resistance in the circuit.
To calculate true power, the voltage and current associated with the resistance must be used. Since the voltage drop across the resistance is equal to the resistance multiplied by the current through the resistance, true power can be calculated by the formula:
True Power = (IR)2R
Where:
True Power: is measured in watts
IR: is resistive current in amperes
R: is resistance in ohms
For example, find the true power of the circuit shown in figure 63.
Since the current in a series circuit is the same in all parts of the circuit:
True Power = (IR)2R
True Power = (5A)2 x 60Ω
True Power = 1500 watts
Calculating Reactive Power in AC Circuits
The reactive power is the power returned to the source by the reactive components of the circuit.
This type of power is measured in Volt-Amperes-Reactive, abbreviated var. Reactive power is calculated by using the voltage and current associated with the circuit reactance.
Since the voltage of the reactance is equal to the reactance multiplied by the reactive current, reactive power can be calculated by the formula:
Reactive Power = (IX)2X
Where:
Reactive power is measured in volt-amperes-reactive.
IX is reactive current in amperes
X is total reactance in ohms
Another way to calculate reactive power is to calculate the inductive power and capacitive power and subtract the smaller from, the larger.
Reactive Power = (IL)2XL – (IC)2XC
Or = (IC)2XC – (IL)2XL
Where:
Reactive power is measured in volt-amperes – reactive
IC is capacitive current in amperes.
XC is capacitive reactance in ohms.
IL is inductive current in amperes.
XL is inductive reactance in ohms.
Either one of these formulas will work. The formula you use depends upon the values you are given in a circuit. For example, find the reactive power of the circuit shown in figure 10 on page 11.
Given:
XL = 30Ω
XC = 110Ω
X = 80Ω
I = 5A
Since this is a series circuit, current (I) is the same in all parts of the circuit.
Solution:
Reactive power = (IX)2X
Reactive power = (5A)2 x 80Ω
Reactive power = 2,000 var
To prove the second formula also works
Reactive power = (Ic)2Xc – (IL)2XL
Reactive power = (5A)2 x 110Ω – (5A)2 x 30Ω
Reactive power = 2,750 var – 750 var
Reactive power = 2,000 var
Calculating Apparent Power in AC Circuits.
Apparent power is the power that appears to the source because of the circuit impedance.
Since the impedance is the total opposition to ac, the apparent power is that power the voltage source “sees.”
Apparent power is the combination of true power and reactive power.
Apparent power is not found by simply adding true power and reactive power, just as impedance is not found by adding resistance and reactance.
To calculate apparent power, you may use either of the following formulas:
Apparent power = (Iz)2Z
Where:
Apparent power is measured in VA (volt-amperes)
IZ is impedance current in amperes
Z is impedance in ohms
Or:
For example, find the apparent power for the circuit shown in figure 64.
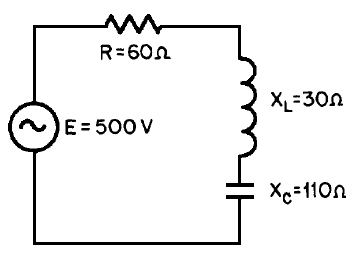
Given:
Z = 100Ω
I = 5A
Recall that current in a series circuit is the same in all parts of the circuit.
Solution:
Apparent power = (Iz)2Z
Apparent power = (5A)2 x 100Ω
Apparent power = 2,500 VA
Or
Power Factor
The POWER FACTOR is a number (represented as a decimal or a percentage) that represents the portion of the apparent power dissipated in a circuit.
If you are familiar with trigonometry, the easiest way to find the power factor is to find the cosine of the phase angle (Θ).
The cosine of the phase angle is equal to the power factor. You do not need to use trigonometry to find the power factor.
Since the power dissipated in a circuit is true power, then:
If true power and apparent power are known, you can use the formula shown above. Going one step further, another formula for power factor can be developed. By substituting the equations for true power and apparent power in the formula for power factor, you get: 
Since current in a series circuit is the same in all parts of the circuit, IR equals IZ. Therefore, in a series circuit,
For example, to compute the power factor for the series circuit shown in figure 10 on page 11, any of the above methods may be used.
If you are familiar with trigonometry, you can use it to solve for angle __ and the power factor.
NOTE: As stated earlier, the power factor can be expressed as a decimal or percentage. In this example, the decimal number .6 could also be expressed as 60%.
Power Factor Correction
The apparent power in an ac circuit has been described as the power the source “sees.” As far as the source is concerned, the apparent power is the power that must be provided to the circuit. You also know that the true power is the power actually used in the circuit.
The difference between apparent power and true power is wasted because, in reality, only true power is consumed. The ideal situation would be for apparent power and true power to be equal.
If this were the case, the power factor would be 1 (unity) or 100 percent.
There are two ways in which this condition can exist.
(1) If the circuit is purely resistive or
(2) if the circuit “appears” purely resistive to the source.
To make the circuit appear purely resistive, there must be no reactance. To have no reactance in the circuit, the inductive reactance (XL) and capacitive reactance (XC) must be equal.
Remember: X = XL – XC
Therefore when XL = XC, X = 0, the expression “correcting the power factor” refers to reducing the reactance in a circuit. The ideal situation is to have no reactance in the circuit.
This is accomplished by adding capacitive reactance to a circuit which is inductive and inductive reactance to a circuit which is capacitive.
For example, the circuit shown in figure 65 has a total reactance of 80 ohms capacitive, and the power factor was .6 or 60 percent.
If 80 ohms of inductive reactance were added to this circuit (by adding another inductor), the circuit would have a total reactance of zero ohms and a power factor of 1 or 100 percent.
The apparent and true power of this circuit would then be equal.
SERIES RLC CIRCUITS
The principles and formulas that have been presented in this chapter are used in all ac circuits.
The examples given have been series circuits.
This lesson section will not present any new material but will be an example of using the principles presented so far.
You should follow each example problem step by step to see how each formula used depends upon the information determined in earlier steps.
When an example calls for solving for square root, you can practice using the square-root table by looking up the values given.
The example series RLC circuit shown in figure 66 will be used to solve for XL, XC, X, Z, IT, true power, reactive power, apparent power, and power factor. The values solved for will be rounded off to the nearest whole number.
First, solve for XL and XC.
Now solve for X
Use the value of X to solve for Z
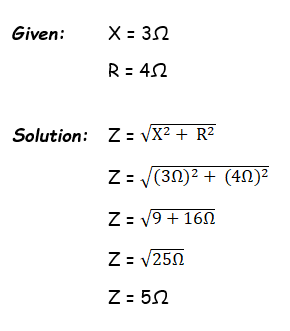This value of Z can be used to solve for total current (IT)
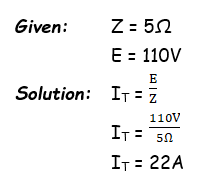
Since current is equal in all parts of a series circuit, the value of IT can be used to solve for the various values of power.
The power factor can now be found using either apparent power and true power or resistance and impedance. The mathematics in this example is easier if you use impedance and resistance.
PARALLEL RLC CIRCUITS
When dealing with a parallel ac circuit, you will find that the concepts presented in this chapter for series ac circuits still apply.
There is one major difference between a series circuit and a parallel circuit that must be considered.
The difference is that current is the same in all parts of a series circuit, whereas voltage is the same across all branches of a parallel circuit.
Because of this difference, the total impedance of a parallel circuit must be computed based on the current in the circuit.
You should remember that in the series RLC circuit, the following three formulas were used to find reactance, impedance, and power factor:
When working with a parallel circuit, you must use the following formulas instead:
NOTE: If no value for E is given in a circuit, any value of E can be assumed to find the values of IL, IC, IX, IR, and IZ.
The same value of voltage is then used to find impedance.
For example, find the value of Z in the circuit shown in figure 67.
Given:
E = 300V
R = 100Ω
XL = 50Ω
XC =150Ω
The first step in solving for Z is to calculate the individual branch currents.
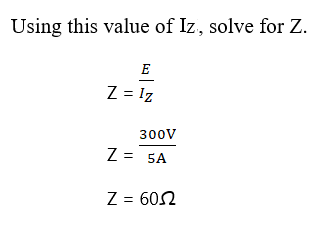
If the value for E were not given and you were asked to solve for Z, any value of E could be assumed. If in the example problem above, you assume a value of 50 volts for E, the solution would be:
Given:
R = 100
XL = 50
XC = 150
E = 50 V (assumed)
When the voltage is given, you can use the values of currents, I R, IX, and IZ, to calculate for the true power, reactive power, apparent power, and power factor.
For the circuit shown in figure 68, the calculations would be as follows.
